Rektlinia sfera projekcio

En geometrio, la rektlinia sfera projekcio aŭ stereografia projekcio estas certa surĵeto (funkcio) kiu projekcias n-sferon de n+1 dimensia eŭklida spaco sur n-hiperebenon. Do ĝi donas hiperebenan bildon de la n-sfero.

En la plej kutima okazo, sfero lokigita en 3-dimensia spaco estas projekciata sur ebenon

La projekcio estas difinita sur la tuta sfero, escepte de unu punkto kiu estas la projekcia punkto. Tie kie ĝi estas difinita, la surĵeto estas glata kaj bijekcia. Ĝi estas ankaŭ konforma en signifo ke ĝi precize prezentas angulajn interrilatojn. Aliflanke, ĝi ne precize prezentas areon, aparte proksime al la projekcia punkto.

Rektlinia sfera projekcio estas uzata en kelkaj partoj de matematiko - en diferenciala geometrio kaj kompleksa analitiko, kaj ankaŭ en kartografio, geologio, kaj kristalografio.

Difino kaj formuloj por kutima dimensio

Rektlinia sfera projekcio de la unuobla sfero de la norda poluso sur la ebeno z = 0, montrita ĉi tie en kruci sekcio.

Ĉi tiu ĉapitro priskribas la projekcion de la unuobla sfero de la norda poluso sur la ebenon tra la ekvatoro. Aliaj variantoj estas traktataj en la sekvaj ĉapitroj.

La unuobla sfero en tri-dimensia spaco R³ estas la aro de punktoj (x, y, z) tiaj ke x² + y² + z² = 1. Estu N = (0, 0, 1) la norda poluso, kaj estu M la cetera parto de la sfero. La ebeno z = 0 situas tra centro de la sfero; la ekvatoro estas la komunaĵo de la sfero kun ĉi tiu ebeno.

Por ĉiu punkto P en M, estas unika linio tra N kaj P, kaj ĉi tiu linio sekcas la ebenon z = 0 en akurate unu punkto P'. La rektlinia sfera projekcio de P esti ĉi tiu punkto P' en la ebeno.

En karteziaj koordinatoj (x, y, z) en la sfero kaj (X, Y) en la ebeno, la projekcio kaj ĝia inverso estas donataj per formuloj

$(X,Y)=\left({\frac {x}{1-z}},{\frac {y}{1-z}}\right),$

$(x,y,z)=\left({\frac {2X}{1+X^{2}+Y^{2}}},{\frac {2Y}{1+X^{2}+Y^{2}}},{\frac {-1+X^{2}+Y^{2}}{1+X^{2}+Y^{2}}}\right).$

La projekcio havas pli simplajn formulojn en la aliaj koordinatsistemoj. En sferaj koordinatoj (φ, θ) sur la sfero (kie φ estas la zenita angulo kaj θ estas la azimuto) kaj polusaj koordinatoj (R, Θ) sur la ebeno, la projekcio kaj ĝia inverso estas donataj per formuloj

$(R,\Theta )=\left({\frac {\sin \varphi }{1-\cos \varphi }},\theta \right),$

$(\varphi ,\theta )=\left(2\arctan \left({\frac {1}{R}}\right),\Theta \right).$

Ĉi tie, φ havas valoro π kiam R = 0. Ankaŭ, estas multaj manieroj reskribi ĉi tiujn formulojnper trigonometriaj identoj. En cilindraj koordinatoj (r, θ, z) sur la sfero kaj polusaj koordinatoj (R, Θ) sur la ebeno, la projekcio kaj ĝia inverso estas donataj per formuloj

$(R,\Theta )=\left({\frac {r}{1-z}},\theta \right),$

$(r,\theta ,z)=\left({\frac {2R}{1+R^{2}}},\Theta ,{\frac {R^{2}-1}{R^{2}+1}}\right).$

Efiko je subaroj de la sfero kaj ebeno

La rektlinia sfera projekcio difinita en la antaŭa sekcio sendas la sudan poluson (0, 0, -1) al (0, 0), la ekvatoron al la unuobla cirklo, la sudan duonsferon al regiono ene la cirklo, kaj la nordan duonsferon al regiono ekster la cirklo.

Sfero kun segmento de rumba linio

La projekcio estas ne difinita je la projekcia punkto N = (0, 0, 1). Malgrandaj najbaraĵoj de ĉi tiu punkto estas sendita al subaroj de la ebeno malproksime de (0, 0). Ju pli proksima P estas al (0, 0, 1), des pli malproksima estas ĝia bildo de (0, 0) en la ebeno. Por ĉi tio onidiras ke la surĵeto de (0, 0, 1) estas la "malfinio" en la ebeno, kaj surĵeto de la sfero estas la ebeno kun aldonita "punkto je malfinio". Ĉi tiu nocio estas utila en projekcia geometrio kaj kompleksa analitiko. Sur nur topologia nivelo, ĝi ilustras ke la sfero estas homeomorfa al la unu punkta kompaktigo de la ebeno.

Rektlinia sfera projekcio konvertas cirklojn en la sfero ne trapasantajn la punkton de la projekcio al cirkloj en la ebeno. Ĝi konvertas cirkloj sur la sfero trapasantajn la punkton de la projekcio al rektaj linioj sur la ebeno. Ĉi tiuj linioj povas esti konsiderataj kiel cirkloj tra la punkto je malfinio, aŭ kiel cirkloj de malfinia radiuso.

Ĉiuj linioj en la ebeno konvertitaj al cirkloj en la sfero per la inverso de la rektlinia sfera projekcio sekcas unu la alian je malfinio. Paralelaj linioj, kiu ne intersekciĝas en la ebeno, estas tangentaj je malfinio. Tial ĉiuj linioj en la ebeno intersekciĝas ie en la sfero, je du punktoj, aŭ tangante je malfinio. Similaj aferoj veras en la reela projekcia ebeno, sed la komunaĵaj interrilatoj estas tie malsamaj.

La rumbaj linioj (aŭ loksodromioj) de la sfero bildiĝas al kurboj en la ebeno de formo

$R=e^{\Theta /a},\,$

kie la parametro a estas la denseco de la rumba linio. Tial rumbaj linioj esti konforma laŭ egalangula spiralo. Ĉi tiuj spiraloj sekcas radiusajn liniojn en la ebeno je egalaj anguloj, ĝuste kiel la rumbaj linioj sekci meridianojn sur la sfero je egalaj anguloj.

Samformeco kaj konservado de areo

Rektlinia sfera projekcio estas konforma bildigo, kio signifas ke ĝi konservas la anguloj je kiuj kurboj krucas unu la alian. Ĉi tiu estas la suba kaŭzo de tio ke rumbaj linioj kaj cirkloj en la sfero bildiĝas al egalangulaj spiraloj kaj cirkloj respektive en la ebeno.

Rektlinia sfera projekcio ne konservas areon. Ĝenerale, la areo de regiono en la sfero ne egalas al areo de ĝia projekcio en la ebeno. La area ero en la ebeno estas donita en karteziaj koordinatoj (X, Y) kiel

$dA={\frac {4}{(1+X^{2}+Y^{2})^{2}}}\;dX\;dY.$

apud la unuobla cirklo X² + Y² = 1, estas ne ŝanĝataj laŭ la areo. Proksime (0, 0) areoj estas ŝanĝataj per faktoro 4 (la areo estas 4-foje pli granda en la sfero ol en la ebeno), kaj proksime al malfinio la areoj estas pli malgrandaj en la sfero, kaj la faktoro proksimiĝas al 0.

Nenio projekcio de sfero al ebeno povas esti samtempe konforma kaj areo-konservanta. Se ĝi ekzistus, tiam ĝi devus esti izometrio kaj devus konservi la gaŭsan kurbecon. Sed la sfero kaj la ebeno havi malsamajn gaŭsa kurbecojn, do ĉi tiu projekcio estas neebla.

Aliaj variantoj

Anstataŭ projekciado al la ekvatora ebeno de la norda poluso, oni povas projekcii de la suda poluso S = (0, 0, −1). La formuloj estas:

$(X,Y)=\left({\frac {x}{1+z}},{\frac {-y}{1+z}}\right),$

$(x,y,z)=\left({\frac {2X}{1+X^{2}+Y^{2}}},{\frac {-2Y}{1+X^{2}+Y^{2}}},{\frac {1-X^{2}-Y^{2}}{1+X^{2}+Y^{2}}}\right).$

Simile al la projekcio de la norda poluso, projekcio de la suda poluso bildigas la ekvatoron al la unuobla cirklo. La inverso de la projekcio de la suda poluso havas la saman orientiĝon sur la sfero kiel la inverso de la projekcio de la norda poluso. Tial la sfero povas esti konsiderata kiel orientita surfaco (2-dimensia sternaĵo) kovrita per du abakoj.

Rektlinia sfera projekcio de la unuobla sfero de la norda poluso sur la ebeno z = -1, montrita ĉi tie en kruca sekcio.

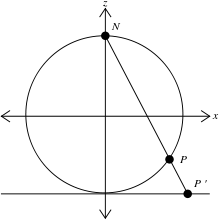
Ankaŭ, povas esti difinita la rektlinia sfera projekcio de la norda poluso (0, 0, 1) al ebeno z = -1, kiu estas tangento al la unuobla sfero je la suda poluso (0, 0, −1). La valoroj X kaj Y produktita per ĉi tiu projekcio estas akurate dufoje pli grandaj ol tiuj produktitaj per la ekvatora projekcio priskribita en la antaŭa ĉapitro. Ĉi tiu projekcio bildigas la ekvatoro al la cirklo de radiuso 2 centrita je (0, 0). La ekvatora projekcio produktas ne malformigas areojn apud la ekvatoro, kaj la tiu poluso-tangenta projekcio anstataŭe produktas ne malformigas areojn je la suda poluso.

Rektlinia sfera projekcio de sfero de punkto Q sur la ebeno E, montrita ĉi tie en kruca sekcio.

Ĝenerale, oni povas difini rektlinian sferan projekcion de ĉiu punkto Q en la sfero al iu ebeno E tia ke

• E estas perpendikulara al la diametro tra Q, kaj
• E ne enhavas na Q.

Tiam por ĉiu punkto P en la sfero kiun ne koincidas kun Q la linio tra P kaj Q krucas ebenon E en akurate unu punkto P^′, kiu estas la rektlinia sfera projekcio de P sur E.

Pli altaj dimensioj

Rektlinia sfera projekcio de regula plurĉelo 24-ĉelo.

Rektlinia sfera projekcio povas ankaŭ esti aplikita al la n-sfero Sⁿ en (n + 1)-dimensia eŭklida spaco E^{n + 1} en la sama maniero. Se Q estas punkto en Sⁿ kaj E estas hiperebeno en E^{n + 1}, tiam la rektlinia sfera projekcio de punkto P ∈ Sⁿ − {Q} estas la punkto P^′ kiu estas komunaĵo de la linio $\scriptstyle {\overline {QP}}$ kun E.

Por kvar-dimensiaj plurĉeloj estadas uzataj jenaj ŝtupoj por fari 2-dimensian bildon (vidu ilustraĵon dekstre):

1. projekcii la plurĉelon al samcentra 3-sfero;
2. per rektlinia sfera projekcio projekcii la 3-sferon kun pentritaj en ĝi verticoj, lateroj kaj edroj al eŭklida 3-spaco;
3. per perspektiva projekcio projekcii la 3-dimensian figuron al 2-dimensia eŭklida ebeno.

Vidu ankaŭ

• Figuro de Schlegel
• Orta projekcio
• Paralela projekcio
• Perspektiva projekcio
• Projekcio
• Stereoskopio

Referencoj

• Apostol, Tom. (1974) Mathematical Analysis - Matematika analitiko, 2‑a eldono, Addison-Wesley.
• Brown, James and Churchill, Ruel. (1989) Complex variables and applications - Komplekso variabloj kaj aplikoj. Novjorko: McGraw-Hill. ISBN 0-07-010905-2.

Eksteraj ligiloj

• http://mathworld.wolfram.com/StereographicProjection.html
• http://planetmath.org/encyclopedia/StereographicProjection.html Arkivigite je 2013-03-10 per la retarkivo Wayback Machine
• Panoramaj Bildaj Projekcioj - Interaga komparo inter diversaj specoj de projekcioj
• Tabelo de ekzemploj kaj propraĵoj de ĉiuj ofte uzataj projekcioj