Listo de unuformaj ebenaj kahelaroj
Ĉi tie estas listigitaj unuformaj kahelaroj da la eŭklida kaj hiperbola ebenoj.
Konveksaj unuformaj kahelaroj de la eŭklida ebeno[redakti | redakti fonton]
Sube estas montritaj la 11 konveksaj unuformaj kahelaroj de la eŭklida ebeno kaj iliaj dualaj kahelaroj.
Estas tri regulaj kaj 8 duonregulaj kahelaroj de la ebeno.
Unuformaj kahelaroj estas listigitaj kun iliaj verticaj konfiguroj, kiu estas vico de edroj kiuj estas ĉirkaŭ ĉiu vertico, ĉiu edro estas priskribita per sia kvanto de lateroj.
Dualaj kahelaroj estas listigitaj per iliaj edraj konfiguroj, kiu estas vico de verticoj kiuj estas ĉirkaŭ ĉiu edro, ĉiu vertico estas priskribita per sia kvanto de lateroj ĉe si.
Ĉi tiuj 11 unuformaj kahelaroj havas 32 malsamajn unuformajn kolorigojn. Unuforma kolorigo permesas al identaj edroj al esti kolorigitaj (kaj konsiderataj) malsame, tamen konservante vertico-transitivecon. Noto: Iu el la bildoj de kahelaroj en ĉi tiu artikolo estas ne unuforme kolorigitaj.
La R3 {4,4} familio[redakti | redakti fonton]
| Unuforma kahelaro | Vertica konfiguro Simbolo de Schläfli Geometria simetria grupo |
Duala kahelaro |
|---|---|---|
 Kvadrata kahelaro (regula) |
4.4.4 {4,4} p4m |
 Mem-duala |
 Senpintigita kvadrata kahelaro |
4.8.8 t{4,4} p4m |
 Kvarlateropiramidigita kvadrata kahelaro |
 Riproĉa kvadrata kahelaro |
3.3.4.3.4 s{4,4} p4g |
 Kaira kvinlatera kahelaro |
La V3 {6,3} familio[redakti | redakti fonton]
| Unuforma kahelaro | Vertica konfiguro Simbolo de Schläfli Geometria simetria grupo |
Duala kahelaro |
|---|---|---|
 Seslatera kahelaro (regula) |
6.6.6 {6,3} t{3,6} p6m |
 Triangula kahelaro |
 Tri-seslatera kahelaro |
3.6.3.6 p6m |
 Kvazaŭregula romba kahelaro |
 Senpintigita seslatera kahelaro |
3.12.12 t{6,3} p6m |
 Trilateropiramidigita triangula kahelaro |
 Triangula kahelaro (regula) |
3.3.3.3.3.3 {3,6} p6m |
 Seslatera kahelaro |
 Malgranda rombo-tri-seslatera kahelaro |
3.4.6.4 p6m |
 Deltosimila tri-seslatera kahelaro |
 Granda rombo-tri-seslatera kahelaro |
4.6.12 p6m |
 Dusekcita seslatera kahelaro |
 Riproĉa seslatera kahelaro |
3.3.3.3.6 s{6,3} p6 |
 Florosimila kvinlatera kahelaro |
Ne konstruebla per konstruo de Wythoff[redakti | redakti fonton]
| Unuforma kahelaro | Vertica konfiguro Simbolo de Schläfli Geometria simetria grupo |
Duala kahelaro |
|---|---|---|
 Plilongigita triangula kahelaro |
3.3.3.4.4 {3,6}:e cmm |
 Prisma kvinlatera kahelaro |
Aldonaj unuformaj kahelaroj[redakti | redakti fonton]
Estas ankaŭ aldonaj unuformaj kahelaroj, kiuj povas esti konsiderataj. Ili havas jenajn diferencojn de la supre listigitaj:
- Kahelaroj kiuj estas analogaj al nekonveksaj unuformaj pluredroj:
- Verticaj figuroj povas havi retroirajn edrojn kaj turniĝi ĉirkaŭ la vertico pli ol unufoje.
- Nekonveksaj stelaj edroj povas esti uzataj.
- Malfiniolateraj edroj {∞} povas esti uzataj.
Entute povas esti konsiderataj 39 unuformaj kahelaroj. sube ili estas donitaj per vertica konfiguro kaj simbolo de Wythoff.
La 3 novaj kahelaroj kun du {∞} edroj:
- ∞.∞ (Du duonebeno (kaheloj, kahelas), malfinia duedro)
- 4.4.∞ - ∞ 2 | 2 (malfinia prismo)
- 3.3.3.∞ - | 2 2 ∞ (malfinia kontraŭprismo)
La 4 novaj kahelaroj, faritaj surbaze iuj el la 11 la bazaj, per anstataŭigo de iuj edroj per {∞} edroj:
- 4.∞.4/3.∞ - 4/3 4 | ∞ (alterna kvadrata kahelaro)
- 3.∞.3.∞.3.∞ - 3/2 | 3 ∞ (alterna triangula kahelaro)
- 6.∞.6/5.∞ - 6/5 6 | ∞ (alterna tri-seslatera kahelaro kun nur seslateroj)
- ∞.3.∞.3/2 - 3/2 3 | ∞ (alterna tri-seslatera kahelaro kun nur trianguloj)
La cetera listo inkluzivas 21 kahelarojn, el ili 7 estas kun {∞} edroj. Estas nur 14 unikaj situoj de lateroj de ĉi tiuj 21 kahelaroj, kaj sube ili estas grupigitaj laŭ situo de lateroj en 14 specojn. La unua speco havas situon de lateroj identan al tiu de 3.4.6.4 kahelaro.
- Speco 1
- 3/2.12.6.12 - 3/2 6 | 6
- 4.12.4/3.12/11 - 2 6 (3/2 3) |
- Speco 2
- 8/3.4.8/3.∞ - 4 ∞ | 4/3
- 8/3.8.8/9.8/7 - 4/3 4 (2 ∞) |
- 8.4/3.8.∞ - 4/3 ∞ | 4
- Speco 3
- 12/5.6.12/5.∞ - 6 ∞ | 6/5
- 12/5.12.12/7.12/11 - 6/5 6 (3 ∞) |
- 12.6/5.12.∞ - 6/5 ∞ | 6
- Speco 4
- 12/5.3.12/5.6/5 - 3 6 | 6/5
- 12/5.4.12/7.4/3 - 2 6/5 (3/2 3) |
- 4.3/2.4.6/5 - 3/2 6 | 2
- Speco 5
- 8.8/3.∞ - 4/3 4 ∞ |
- Speco 6
- 12.12/5.∞ - 6/5 6 ∞ |
- Speco 7
- 8.4/3.8/5 - 2 4/3 4 |
- Speco 8
- 6.4/3.12/7 - 2 3 6/5 |
- Speco 9
- 12.6/5.12/7 - 3 6/5 6 |
- Speco 10
- 4.8/5.8/5 - 2 4 | 4/3
- Speco 11
- 12/5.12/5.3/2 - 2 3 | 6/5
- Speco 12
- 4.4.3/2.3/2.3/2 - ne konstruebla per konstruo de Wythoff
- Speco 13
- 4.3/2.4.3/2.3/2 - riproĉa
- Speco 14
- 3.4.3.4/3.3.∞ - riproĉa
Unuformaj kahelaroj de hiperbola ebeno[redakti | redakti fonton]
La {p,q} familioj[redakti | redakti fonton]
Estas malfinia kvanto da regulaj kahelaroj de la hiperbola ebeno. La kahelaroj povas esti konstruitaj el regulaj konveksaj p-lateroj, kun q el ili ĉirkaŭ ĉiu vertico (do kun simbolo de Schläfli {p,q}), se sumo de la anguloj ĉe vertico estas pli granda ol 360 gradoj (la angula difekto estas negativa). La kondiĉo povas esti skribita kiel
- (p-2)(q-2) > 4
Do povas esti ĉirkaŭ ĉiu vertico:
- Trianguloj - 7 aŭ pli multaj
- Kvadratoj - 5 aŭ pli multaj
- Kvinlateroj - 4 aŭ pli multaj
- Seslateroj - 4 aŭ pli multaj
- p-lateroj (p ≥ 7) - 3 aŭ pli multaj
Surbaze de ili per operacioj povas esti konstruitaj unuformaj neregulaj kahelaroj.
Sube estas montritaj du familioj - {7,3} (3 sepanguloj aŭ 7 trianguloj ĉirkaŭ ĉiu vertico) kaj {5,4} (4 kvinlateroj aŭ 5 kvadratoj ĉirkaŭ ĉiu vertico)
La bildoj estas projekcioj kiel diska modelo de Poincaré.
La {7,3} familio[redakti | redakti fonton]
| Unuforma kahelaro | Vertica konfiguro Simbolo de Schläfli Geometria simetria grupo |
Duala kahelaro |
|---|---|---|
 Ordo-3 seplatera kahelaro (regula) |
7.7.7 {7,3} [7,3] |
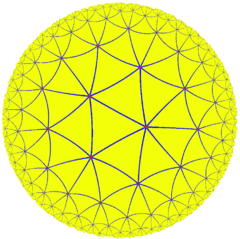 Ordo-7 triangula kahelaro |
 Ordo-3 senpintigita seplatera kahelaro |
3.14.14 t{7,3} [7,3] |
 Ordo-7 trilateropiramidigita triangula kahelaro |
 Tri-seplatera kahelaro |
3.7.3.7 aŭ t1{7,3} [7,3] |
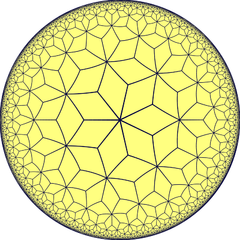 Ordo-7-3 kvazaŭregula romba kahelaro |
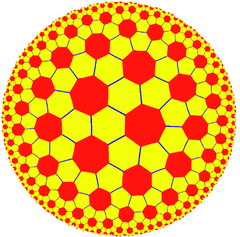 Ordo-7 senpintigita triangula kahelaro |
7.6.6 t{3,7} [7,3] |
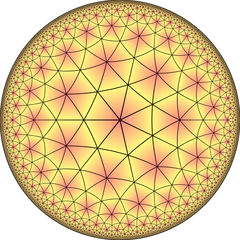 Ordo-3 seplateropiramidigita seplatera kahelaro |
 Ordo-7 triangula kahelaro (regula) |
37 {3,7} [7,3] |
 Ordo-3 seplatera kahelaro |
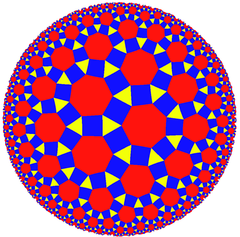 Malgranda rombo-tri-seplatera kahelaro |
3.4.7.4 aŭ t0,2{7,3} [7,3] |
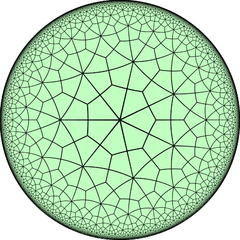 Deltosimila tri-seplatera kahelaro |
 Granda rombo-tri-seplatera kahelaro |
4.6.14 aŭ t0,1,2{7,3} [7,3] |
 Ordo-3 dusekcita seplatera kahelaro |
 Ordo-3 riproĉa seplatera kahelaro (nememspegulsimetria) |
3.3.3.3.7 s{7,3} [7,3] |
 Ordo-7-3 florosimila kvinlatera kahelaro (nememspegulsimetria) |
La {5,4} familio[redakti | redakti fonton]
| Unuforma kahelaro | Vertica konfiguro Simbolo de Schläfli Geometria simetria grupo |
Duala kahelaro |
|---|---|---|
 Ordo-4 kvinlatera kahelaro (regula) |
5.5.5.5 {5,4} [5,4] |
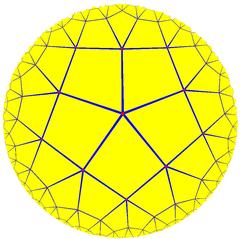 Ordo-5 kvadrata kahelaro |
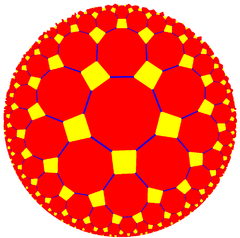 Senpintigita kvinlatera kahelaro |
4.10.10 t{5,4} [5,4] |
 Ordo-5 kvarlateropiramidigita kvadrata kahelaro |
 Kvar-kvinlatera kahelaro |
4.5.4.5 aŭ t1{5,4} [5,4] |
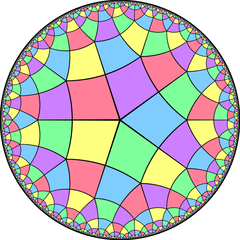 Ordo-5-4 kvazaŭregula romba kahelaro |
 Ordo-5 senpintigita kvadrata kahelaro |
8.8.5 t{3,7} [5,4] |
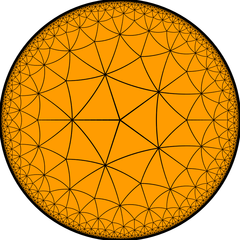 Ordo-4 kvinlateropiramidigita kvinlatera kahelaro |
 Ordo-5 kvadrata kahelaro (regula) |
45 {4,5} [5,4] |
 Ordo-4 kvinlatera kahelaro |
 Malgranda rombo-kvar-kvinlatera kahelaro |
4.4.5.4 aŭ t0,2{5,4} [5,4] |
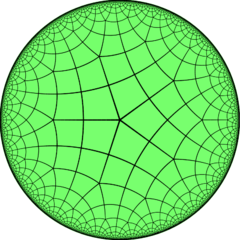 Deltosimila kvar-kvinlatera kahelaro |
 Granda rombo-kvar-kvinlatera kahelaro |
4.8.10 aŭ t0,1,2{5,4} [5,4] |
 Ordo-4 dusekcita kvinlatera kahelaro |
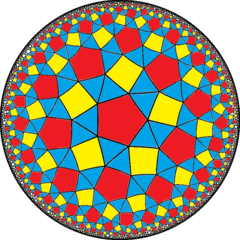 Ordo-4 riproĉa kvinlatera kahelaro (nememspegulsimetria) |
3.3.4.3.5 s{5,4} [5,4] |
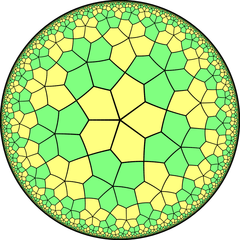 Ordo-5-4 florosimila kvinlatera kahelaro (nememspegulsimetria) |
La (p q r) familioj[redakti | redakti fonton]
Ankaŭ estas familioj konstrueblaj per konstruo de Wythoff kun nombroj (p q r) kun p≥4, q≥3, r≥3 (ne priskribeblaj per simbolo de Schläfli {p,q}).
En ĝenerala okazo ĉi tiaj familioj ne inkluzivas regulajn kahelarojn. Montrita sube aperinta en (4 3 3) familio regula ordo-8 triangula kahelaro fakte respektivas al {8,3} familio.
Sube estas montrita (4 3 3) familio.
La bildoj estas projekcioj kiel diska modelo de Poincaré.
La (4 3 3) familio[redakti | redakti fonton]
| Unuforma kahelaro | Vertica konfiguro Simbolo de Wythoff Geometria simetria grupo |
Duala kahelaro |
|---|---|---|
 Ordo-4-3-3 t0 kahelaro |
(3.4)^3 3 | 3 4 (4 3 3) |
 Ordo-4-3-3 t0 duala kahelaro |
 Ordo-4-3-3 t01 kahelaro |
3.8.3.8 3 3 | 4 (4 3 3) |
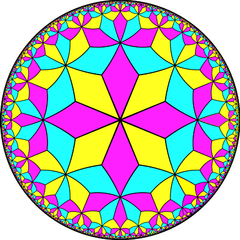 Ordo-4-3-3 t01 duala kahelaro |
 Ordo-4-3-3 t12 kahelaro |
3.6.4.6 4 3 | 3 (4 3 3) |
 Ordo-4-3-3 t12 duala kahelaro |
 Ordo-4-3-3 t2 kahelaro (ordo-8 triangula kahelaro (regula)) |
(3.3)4 4 | 3 3 (4 3 3) |
 Ordo-4-3-3 t2 duala kahelaro (ordo-3 oklatera kahelaro (regula)) |
 Ordo-4-3-3 t012 kahelaro (ordo-8 senpintigita triangula kahelaro) |
6.6.8 4 3 3 | (4 3 3) |
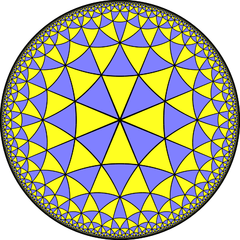 Ordo-4-3-3 t012 duala kahelaro |
 Ordo-4-3-3 riproĉa kahelaro (nememspegulsimetria) |
3.3.3.3.3.4 | 4 3 3 (4 3 3) |
 Ordo-4-3-3 riproĉa duala kahelaro (nememspegulsimetria) |
Vidu ankaŭ[redakti | redakti fonton]
- Konveksa unuforma kahelaro de eŭklida 3-spaco - la 28 unuformo 3-dimensiaj kahelaroj, paralela konstruado al la konveksaj unuformaj Eŭklidaj ebenaj kahelaroj.
Referencoj[redakti | redakti fonton]
- Branko Grünbaum, Shephard G. C.. (1987) Tilings and Patterns - Kahelaroj kaj ŝablonoj. Novjorko: W. H. Freeman. ISBN 0-7167-1193-1. (Ĉapitro 2.1: Regulaj kaj unuformaj kahelaroj, p. 58-65)
Eksteraj ligiloj[redakti | redakti fonton]
- Unuformaj kahelaroj sur la eŭklida ebeno
- Kahelaroj de la ebeno Arkivigite je 2007-09-27 per la retarkivo Wayback Machine
- Mondo de kahelaroj Arkivigite je 2008-06-02 per la retarkivo Wayback Machine
- k-unuformaj kahelaroj Arkivigite je 2006-09-09 per la retarkivo Wayback Machine
- n-unuformaj kahelaroj









