Dutranĉo


En geometrio, dutranĉo estas operacio je regulaj hiperpluredroj kaj regulaj kahelaroj. Ĝi prezentas tranĉon preter rektigon. La originalaj lateroj estas tute perditaj kaj la originalaj edroj restas malgrandigitaj.
Dutranĉitaj regulaj hiperpluredroj kaj kahelaroj povas esti prezentita per etendita simbolo de Schläfli skribmaniero t1, 2{p, q,...}.
En regulaj pluredroj kaj 2-kahelaroj[redakti | redakti fonton]
Por regula pluredro, dutranĉita formo estas la senpintigita duala. Ekzemple, dutranĉita kubo estas senpintigita okedro.
En regulaj plurĉeloj kaj 3-kahelaroj[redakti | redakti fonton]
Por regula plurĉelo, dutranĉita formo estas la sama kiel la dutranĉita duala plurĉelo. Tiel, dutranĉo estas dualo-simetria operacio
Ĉe regula hiperpluredro aŭ kahelaro {p, q, r} ĉeloj {p, q} estas dutranĉitaj en senpintigitajn {q, p} ĉeloj, kaj la verticoj estas anstataŭigitaj per senpintigitaj {q, r} ĉeloj.
Mem-dualaj {p, q, p} plurĉeloj kaj 3-kahelaroj[redakti | redakti fonton]
Kiel rezulto de ĉi tiu operacio farita je mem-dualaj plurĉeloj kaj kahelaroj {p, q, p} aperas ĉelo-transitivaj post dutranĉo plurĉeloj kaj kahelaroj. Estas 5 ĉi tiaj formoj respektivaj al la 5 senpintigitaj regulaj pluredroj t{q, p}. Du el ili estas plurĉeloj, unu estas kahelaro en eŭklida 3-spaco kaj du estas kahelaroj en hiperbola 3-spaco.
| Plurĉelo aŭ kahelaro | Simbolo de Schläfli Figuro de Coxeter-Dynkin |
Speco de ĉelo | Bildo de ĉelo |
|---|---|---|---|
| Dutranĉita 5-ĉelo | t1, 2{3, 3, 3} |
Senpintigita kvaredro | 
|
| Dutranĉita 24-ĉelo | t1, 2{3, 4, 3} |
Senpintigita kubo | 
|
| Dutranĉita kuba kahelaro | t1, 2{4, 3, 4} |
Senpintigita okedro | 
|
| Dutranĉita ordo-3 dudekedra kahelaro | t1, 2{3, 5, 3} |
Senpintigita dekduedro | 
|
| Dutranĉita ordo-5 dekduedra kahelaro | t1, 2{5, 3, 5} |
Senpintigita dudekedro | 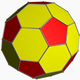
|
Vidu ankaŭ[redakti | redakti fonton]
- Operacioj je hiperpluredroj kaj kahelaroj:
- Tranĉo t0, 1{p, ...}
- Laterotranĉo t0, 2{p, q, ...}
- Lateroverticotranĉo t0, 1, 2{p, q, ...}
- Edrotranĉo t0, 3{p, q, r, ...}
- Edroverticotranĉo t0, 1, 3{p, q, r, ...}
- Edrolaterotranĉo t0, 2, 3{p, q, r, ...}
- Edrolateroverticotranĉo t0, 1, 2, 3{p, q, r, ...}
- Ĉelotranĉo t0, 4{p, q, r, s, ...}
- Entutotranĉo t0, 1, ..., n-1{p1, p2, ..., pn-1}
- Rektigo t1{p, ...}
- Dutranĉo t1, 2{p, q, ...}
- Alternado
- Riproĉigo
- Simbolo de Schläfli - etendita simbolo de Schläfli priskribas rezultojn de la operacioj faritaj je regulaj hiperpluredroj kaj regulaj kahelaroj
