Serio de Taylor
En matematiko, serio de Taylor estas prezento de funkcio kiel serio (malfinia sumo de termoj kalkulitaj laŭ valoroj de derivaĵoj de la funkcio je sola punkto. Se la punkto kie estas kalkulitaj derivaĵoj estas nulo, la serio estas nomata ankaŭ kiel serio de Maclaurin.
Difino[redakti | redakti fonton]
La serio de Taylor de reela aŭ kompleksa funkcio f(x), kiu estas malfinie diferencialebla en najbaraĵo de nombro a, estas la potencoserio
aŭ la samo alie skribita:
kie n! estas la faktorialo de n
- f(n)(a) estas la n-a derivaĵo de f komputita je punkto a; la nula derivaĵo de f estas difinita kiel la f mem.
Ĉi tie estas uzataj (x-a)0=1 kaj 0!=1.
Sub certaj kondiĉoj (vidu sube), serio de Taylor de f(x) egalas al f(x) mem por ĉiuj x sufiĉe proksimaj al a.
Proprecoj[redakti | redakti fonton]
Serio de Taylor ne estas ĝenerale nepre konverĝa serio, sed ofte estas. La limigo de konverĝa serio de Taylor de funkcio f ĝenerale ne nepre estas egalas al la funkcia valoro f(x), sed ofte ĝi estas. Se ĉi tiu serio konverĝas por ĉiu x en najbaraĵo de a (en la intervalo (a-r, a+r)) kaj la sumo estas egala al f(x), la funkcio estas nomata kiel analitika funkcio en ĉi tiu najbaraĵo. Se f(x) estas egala al ĝia serio de Taylor ĉie ĝi estas nomata kiel tuta funkcio.
La eksponenta funkcio , sinuso sin x kaj kosinuso cos x estas tutaj funkcioj.
La logaritmo, tangento kaj tangentarko ne estas tutaj funkcioj. Por ĉi tiuj funkcioj la serio de Taylor ne konverĝas se x estas sufiĉe malproksime de a.
 La sinusa funkcio sin(x) (blua) estas aproksimita per ĝia polinomo de Taylor de ordo 7 (roza) por plena periodo centrita ĉirkaŭ la punkto a = 0. La roza kurbo estas la polinomo de ordo 7:
Pro tio ke signoj de termoj estas alternaj, la eraro de ĉi tiu proksimuma kalkulado estas ne pli granda ol la unua forĵetita termo . Tiel por |x|<1, la eraro estas ne pli granda ol 3·10−6. |
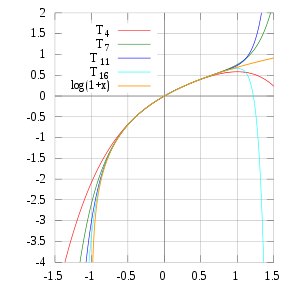 La polinomoj de Taylor por log(1+x). En kontrasto al sinuso, ĉi tiuj proksimumigoj konverĝas al la funkcio nur por -1 < x ≤ 1. Por x > 1, la polinomo de Taylor de pli alta grado estas pli malbona proksimumigo. Ĉi tio estas ekzemplo de fenomeno de Runge. |
Serio de Taylor povas esti uzata por kalkuli la valoron de la funkcio en la respektiva regiono. La partaj sumoj (la polinomoj de Taylor) de la serio povas esti uzataj kiel proksimumigoj de la funkcio (eble per reordigo de la polinomo en la formon de Ĉebiŝev kaj komputo per la algoritmo de Clenshaw). Ili estas sufiĉe bonaj se sufiĉe multaj termoj estas inkluzivitaj.
La teoremo de Taylor donas diversaj de ĝeneralaj baroj pri la amplekso de la eraro de aproksimado de funkcio per ĝia polinomo de Taylor de iu ordo.
La seria prezento plisimpligas multaj matematikajn pruvojn.
La plej simpla pruvo de eŭlera formulo estas per la serioj de Taylor por sinuso, kosinuso, kaj eksponento.
Diferencialado kaj integralado de potencoserio povas esti plenumita aparte por ĉiu termo kaj estas facilaj. Analitika funkcio povas esti unike etendita al holomorfa funkcio difinita en malfermita disko en la kompleksa ebeno.

Ekzistas malfinie diferencialeblaj funkcioj f(x) kies serio de Taylor konverĝi, sed estas ne egala al f(x). Ekzemple, la funkcio difinita kiel f(x) = e-1/x² se x≠0 kaj f(0) = 0 estas ekzemplo de ne-analitika glata funkcio. Ĉiuj ĝiaj derivaĵoj je x=0 estas nuloj , tiel la serio de Taylor de f(x) je a=0 estas nulo ĉie, kvankam la funkcio estas nenula por ĉiu x≠0. Ĉi tio ne estadas ĉe serio de Taylor en kompleksa analitiko. En kompleksa ebeno, la areo de konverĝo de serio de Taylor estas ĉiam disko (eble kun radiuso 0), kaj se la serio de Taylor konverĝas, ĝi konverĝas al la funkcia valoro. La funkcio f(z) = e-1/x² ne proksimiĝas al 0 se z proksimiĝas al 0 laŭ la imaginara akso, do ĉi tiu funkcio estas ne kontinua en 0 se ĝi estas konsiderata kiel funkcio de kompleksa variablo.
Pro tio ke ĉiu vico de reela aŭ kompleksaj nombroj povas aperi kiel koeficientoj en la serio de Taylor de malfinie diferencialebla funkcio difinis sur la reela linio, la konverĝa radiuso de serio de Taylor povas esti nulo. Estas eĉ malfinie diferencialeblaj funkcioj difinitaj sur la reela linio kies serio de Taylor havas konverĝan radiuson 0 ĉie.
Iuj funkcioj ne povas esti skribita kiel serio de Taylor ĉar ili havi specialaĵojn; en ĉi tiuj okazoj tamen povas ekzisti seria prezento se konsideri ankaŭ negativajn potencojn de la variablo, vidu en serio de Laurent. Kaj la pli supre konsiderata funkcio f(x) = e-1/x² povas esti skribita kiel serio de Laurent.
Serioj de Taylor de iuj funkcioj[redakti | redakti fonton]





La serioj en ĉi tiu ĉapitro estas je a=0, se ne estas skribite alie. Ili estas validaj ankaŭ por kompleksaj valoroj de x.
La serio por ĉiu polinomo estas la polinomo mem.
La serio por la eksponenta funkcio ex estas (ĉar ĉiuj derivaĵoj de ex estas ex mem, kaj je 0 ili ĉiuj egalas al 1):
-
- .
- kie Bj estas nombroj de Bernoulli.
- kie Ej estas eŭleraj nombroj.
- kie Bj estas nombroj de Bernoulli.
Binomo de Newton, inkluzivas la malfinian geometrian serion por α = -1 kaj la kvadratan radikon por α = 1/2:
- kie estas ĝeneraligitaj simboloj de Newton
Malfinia geometria serio:
Variantoj de la malfinia geometria serio:
- la serio je a=1 por estas
- (por 0 < x < 2 por reela x)
Finia geometria serio:
La serio je a=0 por estas ricevata per integraligo de la pli supre donita serio por :
do la serio por je a=1 estas
- (por 0 < x < 2 por reela x)
Serio de Taylor en kelkaj variabloj[redakti | redakti fonton]
La serio de Taylor povas esti ĝeneraligita al funkcio de pli ol unu variablo
-
- .
En la mult-indeksa skribmaniero la serio de Taylor por kelkaj variabloj estas
Ekzemple por funkcio de 2 variabloj x kaj y, la serio de Taylor ĝis la 2-a ordo je la punkto (a, b) estas:
kie la subaj indicoj signifas la respektivajn partajn derivaĵojn.
La serio de Taylor ĝis la 2-a ordo povas esti skribita kiel
kie estas la gradiento (matematiko) kaj estas la matrico de Hessian.
Serioj de Taylor kiel difinoj[redakti | redakti fonton]
Klasike, algebraj funkcioj estas difinita per algebra ekvacio, kaj transcendaj funkcioj estas difinitaj per iuj propraĵoj.
Tamen, ankaŭ serioj de Taylor estas uzitaj por difini iujn funkcion, ekzemple tiel estas difinitaj matrica eksponenta funkcio kaj matrica logaritmo. Sinuso kaj kosinuso povas esti ankaŭ tiel difinitaj.
Vidu ankaŭ[redakti | redakti fonton]
Eksteraj ligiloj[redakti | redakti fonton]
- Eric W. Weisstein, Serio de Taylor en MathWorld.
- Madhava de Sangamagramma Arkivigite je 2010-04-18 per la retarkivo Wayback Machine
- [1]
- Maniero de Parker-Sochacki Arkivigite je 2005-12-02 per la retarkivo Wayback Machine
- [2] Arkivigite je 2006-11-17 per la retarkivo Wayback Machine
- Videbligo Arkivigite je 2007-06-05 per la retarkivo Wayback Machine kie eblas elekti la punkton de la proksimumigo kaj la kvanton de derivaĵoj









































![{\displaystyle +{\frac {1}{2!}}[f_{xx}(a,b)(x-a)^{2}+2f_{xy}(a,b)(x-a)(y-b)+f_{yy}(a,b)(y-b)^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec3ded454642ca847cdece3d2aba5fa65193555)


