Trigonometria funkcio
publikigita versio estis patrolita je 4 dec. 2023. Estas kontrolendaj ŝanĝoj de ŝablonoj/dosieroj.
Ŝanĝoj al ŝablonoj aŭ dosieroj en ĉi tiu versio estas kontrolendaj. La stabila versio estis patrolita je 4 dec. 2023.
| Matematikaj funkcioj |
|---|
| fonta aro, cela aro • bildo, malbildo • bildaro, argumentaro |
| Fundamentaj funkcioj |
| Algebraj funkcioj: konstanta • lineara • kvadrata • polinoma • racionala • Transformo de Möbius Aliaj funkcioj: trigonometriaj • inversa trigonometria • hiperbola • eksponenta • logaritma • potenca |
| Specialaj funkcioj |
| erara • β • Γ • ζ • η • W de Lambert • de Bessel |
| Nombroteoriaj funkcioj: |
| τ • σ • de Möbius • φ • π • λ |
| Ecoj: |
| totaleco kaj parteco • pareco kaj malpareco • monotoneco • bariteco • periodeco • disĵeteco • surĵeteco • dissurĵeteco kontinueco • derivaĵeco • integralebleco |
En matematiko, la trigonometriaj funkcioj estas ses funkcioj de angulo.
Ili estas ekvivalente difinebla laŭ diversaj manieroj.
- Geometriaj difinoj:
- Rilatumoj inter lateroj de orta triangulo enhavantaj la angulon, ĉi tio donas difinon por reelaj valoroj de la variablo inter 0 kaj π/2 (orto).
- Longoj de diversaj segmentoj de unuocirklo, ĉi tio donas difinon por ĉiuj reelaj valoroj de la variablo (krom iuj certaj valoroj por iuj el la funkcioj).
- Algebraj difinoj:
- Malfiniaj serioj
- Solvaĵoj de certaj diferencialaj ekvacioj, ĉi tio donas vastigaĵon al kompleksaj valoroj de la variablo (krom iuj certaj valoroj por iuj el la funkcioj).
Por ke la geometriaj kaj la algebraj difinoj donu koincidantajn rezultojn, la angulo θ devas esti mezurita en radianoj.
La difino per orta triangulo senpere donas ĉiujn ses funkciojn. En iuj el la aliaj okazaj komence estas difinataj ne ĉiuj funkcioj (sin kaj cos tamen estas difinataj), la aliaj funkcioj estas tiam difinataj per formuloj de kolumno "Ĉefa idento" de la tabelo pli supre.
Skribmanieroj kaj grafikaĵoj[redakti | redakti fonton]
| Nomo | Kutima skribmaniero | Ĉefa idento | Limigoj de valoro por reela argumento | Periodo |
|---|---|---|---|---|
| sinuso | y = sin θ | −1 ≤ y ≤ 1 | 2π | |
| kosinuso | y = cos θ | −1 ≤ y ≤ 1 | 2π | |
| tangento | y = tan θ aŭ y = tg θ |
tan θ = sin θ / cos θ | ĉiuj reelaj y | π |
| kotangento | y = cot θ aŭ y = cotan θ aŭ y = ctg θ |
cot θ = cos θ / sin θ | ĉiuj reelaj y | π |
| sekanto | y = sec θ | sec θ = 1 / cos θ | −∞ < y ≤ −1 aŭ 1 ≤ y < ∞ | 2π |
| kosekanto | y = csc θ aŭ y = cosec θ |
csc θ = 1 / sin θ | −∞ < y ≤ −1 aŭ 1 ≤ y < ∞ | 2π |
 Grafikaĵoj de sin x kaj cos x |
 Grafikaĵo de tan x |
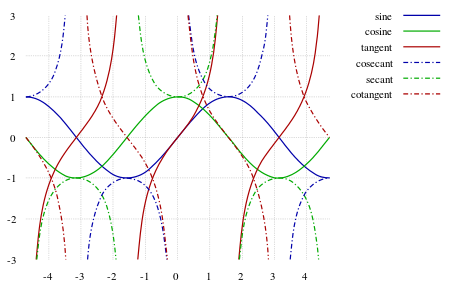 Sinuso, Kosinuso, Tangento, Kosekanto (punktita), Sekanto (punktita), Kotangento (punktita) |
Difinoj per orta triangulo[redakti | redakti fonton]

Trigonometriaj funkcioj estas difinataj per anguloj de orta triangulo per rilatumoj inter longoj de ĝiaj lateroj.
En orta triangulo, la funkcioj de angulo α egalas al rilatumoj inter longoj de la lateroj:
Difinoj per unuocirklo[redakti | redakti fonton]


Estu la unuocirklo, la cirklo de radiuso unu centrita je la fonto. De la teoremo de Pitagoro la ekvacio de la unuocirklo estas:
Estu duonrekto el la fonto (0,0) kun angulo de θ kun la pozitiva duono de la x-akso. La linio sekcas la unuocirklon en punkto, kies x kaj y koordinatoj estas cos θ kaj sin θ respektive.
Por , orta triangulo povas esti konstruita per aldono de perpendikularo el la punkto (x, y) al la x-akso. La triangulo-hipotenuzo de longo egala al radiuso de la cirklo, do egalas al la 1. Longoj de la du aliaj lateroj estas x kaj y. Tiel kaj , kio koincidas kun la difino per orta triangulo,
Por anguloj pli grandaj ol 2π aŭ malpli grandaj ol -2π, oni simple daŭre turnu la punkton ĉirkaŭ la cirklo. Do, sinuso kaj kosinuso estas periodaj funkcioj kun periodo 2π:
por ĉiu angulo θ kaj ĉiu entjero k.
La plej malgranda pozitiva periodo, aŭ la primitivo periodo de la funkcio, por sinuso, kosinuso, sekanto kaj kosekanto estas plena cirklo, 2π radianoj aŭ 360 gradoj; la primitivo periodo de tangento kaj aŭ kotangento estas nur duono de cirklo, kio estas π radianoj aŭ 180 gradoj.
Valoro de tangento ŝanĝiĝas malrapide ĉirkaŭ anguloj de kπ, sed ŝanĝi rapide je anguloj proksimaj al .
La grafikaĵo de la tangento havas vertikalajn asimptotojn je . En ĉi tiuj okazo la funkcio proksimiĝas al plus malfinio kiam θ proksimiĝas al de maldekstro kaj la funkcio proksimiĝas al minus malfinio kiam θ proksimiĝas al de dekstro.
Difinoj per malfiniaj serioj[redakti | redakti fonton]

Uzante nur geometrion kaj proprecojn de limesoj, eblas montri ke derivaĵo de sinuso estas kosinuso kaj derivaĵo de kosinuso estas negativo de sinuso. (la variablo estas mezurita en radianoj). Do la serioj de Taylor estas:
Interrilato kun eksponenta funkcio kaj kompleksaj nombroj[redakti | redakti fonton]



El la serioj sekvas ke la sinuso kaj kosinuso estas respektive la imaginara parto kaj la reela parto de la eksponenta funkcio, kiam ĝia argumento estas pure imaginara:
Kaj
Ĉi tiu idento estas la eŭlera formulo en kompleksa analitiko. Ĝi priskribas la unuoblan cirklon en la kompleksa ebeno.
Plue, la serioj permesas difinon por kompleksaj argumentoj z:
kie i2 = -1.
Difinoj per diferencialaj ekvacioj[redakti | redakti fonton]
Ambaŭ la sinuso kaj kosinuso kontentigas la diferencialan ekvacion
En la 2-dimensia funkcia spaco V konsistanta el ĉiuj solvaĵoj de ĉi tiu ekvacio, la sinusa funkcio estas la unika solvaĵo kun la komencaj kondiĉoj y(0) = 0 kaj y′(0) = 1, kaj la kosinuso estas la unika solvaĵo kun la komencaj kondiĉoj y(0) = 1 kaj y′(0) = 0. Pro tio ke sinuso kaj kosinuso estas lineare sendependaj, kune ili formas bazon de V. Tio ke sinuso kaj kosinuso kontentigas al signifas ke ili estas propraj funkcioj de la dua-derivaĵa operatoro.
La tangento estas la unika solvaĵo de la nelineara diferenciala ekvacio
kun la komenca kondiĉo y(0) = 0.
Signifo de radianoj[redakti | redakti fonton]
Radiano estas tia mezurunuo de angulo, kun kiu sinuso kaj kosinuso kontentigas la diferencialan ekvacion
Se argumento al sinuso aŭ kosinuso en radianoj estas skalita per koeficiento,
do la derivaĵo estas skalita per la amplitudo:
Ĉi tie, k estas konstanto kiu prezentas surĵeto inter unuoj. Se x estas en gradoj, tiam
Ĉi tiu signifas ke dua derivaĵo de sinuso en gradoj kontentigas diferencialan ekvacion
La kosinusa dua derivaĵo kondutas simile.
Proprecoj[redakti | redakti fonton]
Nulvaloroj[redakti | redakti fonton]
Fazrilatoj inter la unuopaj funkcioj[redakti | redakti fonton]
Multoblaj anguloj[redakti | redakti fonton]
| Duoblaj anguloj | |||
|---|---|---|---|
| Trioblaj anguloj | |||
| n-oblaj anguloj: | |||
| Duonaj anguloj | |||
Pri tangento kaj kotangento ekzistas rilato inter n+1-obla kaj n-obla argumento:
Derivaĵo kaj malderivaĵo[redakti | redakti fonton]
La derivaĵon kaj la malderivaĵon montras la sekva tabelo.
| Derivaĵo | Nedifinita integralo | |
|---|---|---|
| (por reela x) | ||
| (por reela x) | ||
| (por reela x) | ||
| (por reela x) |
Difinoj per funkciaj ekvacioj[redakti | redakti fonton]
Oni povas difini la trigonometriajn funkciojn surbaze de iuj el iliaj propraĵoj. Ekzistas akurate unu paro de reelaj funkcioj sin kaj cos tia ke por ĉiuj reelaj nombroj x kaj y jenaj ekvacioj veras:
kun la aldona kondiĉo ke
Periodaj funkcioj[redakti | redakti fonton]
Sinuso kaj kosinuso povas esti uzataj por studi ajnajn periodaj funkcioj. Ĉiu perioda funkcio de reela variablo povas esti skribita kiel malfinia sumo de sinuso kaj kosinuso de malsamaj frekvencoj; ĉi tiu estas la baza ideo de analizo de Fourier.
Por funkcio f(x) kun periodo a 2π, estu la koeficientoj de Fourier:
Tiam la malfinia serio sub certaj kondiĉoj konverĝas al la fonta funkcio f(x):
Ekzemple la kvadrata ondo povas esti skribita kiel la serio de Fourier:
(ĉi tie ĉiuj an kaj duono da bn estas nuloj)
Kalkulado[redakti | redakti fonton]
La kalkulado de trigonometriaj funkcioj estas ampleksa temo. La unua paŝo en komputado de trigonometriaj funkcioj estas limiga malpligrandigo – malpligrandigo de la donita angulo al "malpligrandigita angulo" en iu certas malgranda limigo de anguloj, ekzemple 0 kaj π/2, uzanta periodecon kaj simetriojn de la trigonometriaj funkcioj.
Fruaj komputiloj tipe komputis trigonometriajn funkciojn per interpolo inter valoroj de anticipe donitaj tabeloj de iliaj valoroj. Ĉi tiaj tabeloj estas tipe generataj per ripetita apliko de la duon-angula kaj angulo-adiciaj formuloj, startanta de sciata valoro (ekzemple ).
Modernaj komputiloj uzas diversajn teknikojn. Unu komuna maniero estas proksimuma kalkulado per polinomo aŭ racionala funkcio (ekzemple proksimuma kalkulado de Ĉebiŝev, plej bona uniforma proksimuma kalkulado, kaj proksimuma kalkulado de Padé, kaj tipe por pli bona precizeco serio de Taylor kaj serio de Laurent). Kutime la plej proksima angulo estas prenita de malgranda tabelo, kaj poste la polinomo estas uzata por komputi la korektigaĵon.
Sur pli simplaj aparatoj ĉe kiuj mankas aparataraj multiplikantoj, estas algoritmo CORDIC kaj similaj, kiuj uzas nur ŝovojn kaj adiciojn.
Por tre alte precizaj kalkuloj, kiam seria elvolvaĵa konverĝo iĝas malrapidan, trigonometriaj funkcioj povas esti aproksimita per la aritmetiko-geometria meznombro, kiu aproksimas la trigonometria funkcio per la (kompleksa) elipsa integralo.[1]
Por iuj simplaj anguloj, la valoroj povas esti facile komputita permane uzanta la teoremo de Pitagoro, kiel en jenaj ekzemploj. Valoroj de la funkcioj por ĉiu entjera oblo de π/60 (3°) povas troviĝi akurate.
Estu orta triangulo kie la du aliaj anguloj estas egalaj, kaj pro tio estas ambaŭ π/4. Tiam la longoj de katetoj a kaj b estas interegalaj, estu a = b = 1. La valoroj de sinuso, kosinuso kaj tangento de π/4 povas tiam troviĝi per la teoremo de Pitagoro:
kaj do:
Por kalkuli la funkciojn de anguloj π/3 (60°) kaj π/6 (30°), oni startu de egallatera triangulo kun latera longo 1. Ĉiuj ĝiaj anguloj estas π/3. Per divido de ĝi per mediano, rezultiĝas du ortaj trianguloj ĉi kun anguloj π/6 kaj π/3. Ĉe ĉiu el ĉi tiuj ortaj trianguloj, longo de la plej mallonga kateto estas 1/2, longo de la alia kateto estas (√3)/2 kaj longo de la hipotenuzo estas 1. Do:
Vidu ankaŭ[redakti | redakti fonton]
- Inversa trigonometria funkcio
- Funkcioj coversin, haversin, hacoversin, versin
- Teoremo de Pitagoro
- Listo de trigonometriaj identoj
- Pruvoj de trigonometriaj identoj
- Leĝo de sinusoj
- Leĝo de kosinusoj
- Leĝo de tangentoj
- Sfera leĝo de kosinusoj
- Eŭlera formulo
- Ĉenfrakcio de Gaŭso - ĉenfrakcia difino por tangento
- Hiperbola funkcio
- Inversa hiperbola funkcio
- Funkcio de Gudermannian
Referencoj[redakti | redakti fonton]
Eksteraj ligiloj[redakti | redakti fonton]
- http://www.visionlearning.com/library/module_viewer.php?mid=131&l=&c3=
- Maor, Eli, Trigonometrio Arkivigite je 2006-04-14 per la retarkivo Wayback Machine, ISBN 0-691-09541-8.
- Needham, Tristan, "Enkonduko" Arkivigite je 2004-06-02 per la retarkivo Wayback Machine" al Vida Kompleksa Analitiko Arkivigite je 2008-06-07 per la retarkivo Wayback Machine. (1999). ISBN 0-19-853446-9.
- O'Connor, J.J., kaj E.F. Robertson, Trigonometriaj funkcio.
- O'Connor, J.J., kaj E.F. Robertson, "Madhava de Sangamagramma" Arkivigite je 2006-02-26 per la retarkivo Wayback Machine.
- Pearce, Ian G., "Madhava de Sangamagramma" Arkivigite je 2006-05-05 per la retarkivo Wayback Machine.
- Tangento je MathWorld.
| ||||||||||
















































































![{\displaystyle f(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }[a_{n}\cos(nx)+b_{n}\sin(nx)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a03aa68810765bc20dd6b0c6f4f7ffc1c06c433)







