En matematiko , la inversaj trigonometriaj funkcioj estas la retroĵetoj de la trigonometriaj funkcioj . La ĉefaj estas jenaj:
Nomo
Kutima skribmaniero
Difino
Domajno de x por reela rezulto
Limigoj de kutima ĉefa valoro
Sinusarko
y = arcsin(x) x = sin (y) −1 ≤ x ≤ 1 −π/2 ≤ y ≤ π/2
Kosinusarko
y = arccos(x) x = cos (y) −1 ≤ x ≤ 1 0 ≤ y ≤ π
Tangentarko
y = arctan(x) aŭ y = arctg(x) x = tan (y) ĉiuj reelaj x
−π/2 < y < π/2
Kotangentarko
y = arccot(x) aŭ y = arccotan(x) aŭ y = arcctg(x) x = cot (y) ĉiuj reelaj x
0 < y < π
Sekantarko
y = arcsec(x) x = sec (y) −∞ < x ≤ −1 aŭ 1 ≤ x < ∞ 0 ≤ y < π/2 aŭ π/2 < y ≤ π
Kosekantarko
y = arccsc(x) aŭ y = arccosec(x) x = csc (y) −∞ < x ≤ −1 aŭ 1 ≤ x < ∞ −π/2 ≤ y < 0 aŭ 0 < y ≤ π/2
Se x estas permesita al esti kompleksa nombro , tiam la supre donitaj limigoj de y aplikas nur al reelaj x .
La skribmaniero sin−1 , cos−1 , ktp estas ofte uzata por arcsin, arccos , ktp.
ĉefaj valoroj de la arcsin(x) kaj arccos(x)
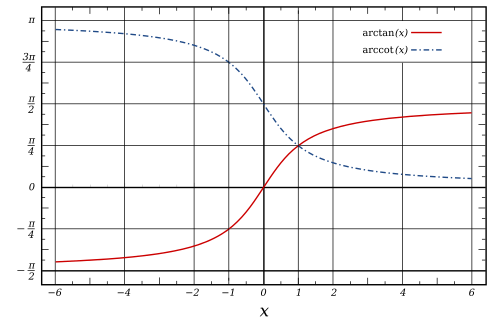
arctan(x) kaj arccot(x)
arcsec(x) kaj arccsc(x)
En komputilaj programlingvoj la funkcioj arcsin, arccos, arctan estas kutime nomataj kiel asin, acos, atan . Multaj programlingvoj ankaŭ provizas la du-argumentan funkcion atan2 , vidu sube pri ĝi.
Interrilatoj inter la inversaj trigonometriaj funkcioj [ redakti | redakti fonton ] Komplementoj :
arccos x = π/2 - arcsin x arccot x = π/2 - arctan x arccsc x = π/2 - arcsec x Negativaj argumentoj:
arcsin (-x) = - arcsin x arccos (-x) = π - arccos x arctan (-x) = - arctan x arccot (-x) = π - arccot x arcsec (-x) = π - arcsec x arccsc (-x) = - arccsc x Inversaj argumentoj:
arccos (1/x) = arcsec x arcsin (1/x) = arccsc x arctan (1/x) = π/2 - arctan x = arccot x , se x > 0 arctan (1/x) = -π/2 - arctan x = -π + arccot x , se x < 0 arccot (1/x) = π/2 - arccot x = arctan x , se x > 0 arccot (1/x) = 3π/2 - arccot x = π + arctan x , se x < 0 arcsec (1/x) = arccos x arccsc (1/x) = arcsin x Per arcsin :
arccos
x
=
arcsin
1
−
x
2
,
{\displaystyle \arccos x=\arcsin {\sqrt {1-x^{2}}},}
0
≤
x
≤
1
{\displaystyle \ 0\leq x\leq 1}
arctan
x
=
arcsin
x
x
2
+
1
{\displaystyle \arctan x=\arcsin {\frac {x}{\sqrt {x^{2}+1}}}}
Rimarku ke kiam la kvadrata radiko de kompleksa nombro estas uzata ĉi tie, oni elektu la ĉefan valoron de la radiko (kun la pozitiva reela parto se imaginara parto estas nulo, alia kun la pozitiva imaginara parto).
De la tangenta duono-angula formulo
tan
θ
2
=
sin
θ
1
+
cos
θ
{\displaystyle \tan {\frac {\theta }{2}}={\frac {\sin \theta }{1+\cos \theta }}}
arcsin
x
=
2
arctan
x
1
+
1
−
x
2
{\displaystyle \arcsin x=2\arctan {\frac {x}{1+{\sqrt {1-x^{2}}}}}}
arccos
x
=
2
arctan
1
−
x
2
1
+
x
{\displaystyle \arccos x=2\arctan {\frac {\sqrt {1-x^{2}}}{1+x}}}
−
1
<
x
≤
+
1
{\displaystyle -1<x\leq +1}
arctan
x
=
2
arctan
x
1
+
1
+
x
2
{\displaystyle \arctan x=2\arctan {\frac {x}{1+{\sqrt {1+x^{2}}}}}}
arctan
u
+
arctan
v
=
arctan
(
u
+
v
1
−
u
v
)
{\displaystyle \arctan u+\arctan v=\arctan \left({\frac {u+v}{1-uv}}\right)}
Pro la pruvo, startu de
tan
(
α
+
β
)
=
tan
α
+
tan
β
1
−
tan
α
tan
β
{\displaystyle \tan(\alpha +\beta )={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}\,}
kaj estu
u
=
tan
α
,
v
=
tan
β
.
{\displaystyle u\,=\,\tan \,\alpha \,,\,v=\,\tan \,\beta .}
Ĉiu trigonometriaj funkcioj estas periodaj en la reela parto de ĝia argumento, trapasanta ĉiujn siajn valorojn dufoje en ĉiu intervalo de 2π . Ĉi tiu periodeco estas montrita en la ĝeneralaj inversoj:
sin y = x se kaj nur se y = arcsin x + 2kπ aŭ y = π − arcsin x + 2kπ por iu entjero k .cos y = x se kaj nur se y = arccos x + 2kπ aŭ y = − arccos x + 2kπ por iu entjero k .tan y = x se kaj nur se y = arctan x + kπ por iu entjero k .cot y = x se kaj nur se y = arccot x + kπ por iu entjero k .sec y = x se kaj nur se y = arcsec x + 2kπ aŭ y = − arcsec x + 2kπ por iu entjero k .csc y = x se kaj nur se y = arccsc x + 2kπ aŭ y = π − arccsc x + 2kπ por iu entjero k .Derivaĵoj de inversaj trigonometriaj funkcioj [ redakti | redakti fonton ] Simplaj derivaĵoj de inversaj trigonometriaj funkcioj por reelaj kaj kompleksaj argumentoj estas:
d
d
x
arcsin
x
=
1
1
−
x
2
{\displaystyle {\frac {d}{dx}}\arcsin x={\frac {1}{\sqrt {1-x^{2}}}}}
d
d
x
arccos
x
=
−
1
1
−
x
2
{\displaystyle {\frac {d}{dx}}\arccos x={\frac {-1}{\sqrt {1-x^{2}}}}}
d
d
x
arctan
x
=
1
1
+
x
2
{\displaystyle {\frac {d}{dx}}\arctan x={\frac {1}{1+x^{2}}}}
d
d
x
arccot
x
=
−
1
1
+
x
2
{\displaystyle {\frac {d}{dx}}\operatorname {arccot} x={\frac {-1}{1+x^{2}}}}
d
d
x
arcsec
x
=
1
x
2
1
−
1
x
2
{\displaystyle {\frac {d}{dx}}\operatorname {arcsec} x={\frac {1}{x^{2}\,{\sqrt {1-{\frac {1}{x^{2}}}}}}}}
d
d
x
arccsc
x
=
−
1
x
2
1
−
1
x
2
{\displaystyle {\frac {d}{dx}}\operatorname {arccsc} x={\frac {-1}{x^{2}\,{\sqrt {1-{\frac {1}{x^{2}}}}}}}}
Nur por reelaj argumentoj:
d
d
x
arcsec
x
=
1
|
x
|
x
2
−
1
{\displaystyle {\frac {d}{dx}}\operatorname {arcsec} x={\frac {1}{|x|\,{\sqrt {x^{2}-1}}}}}
d
d
x
arccsc
x
=
−
1
|
x
|
x
2
−
1
{\displaystyle {\frac {d}{dx}}\operatorname {arccsc} x={\frac {-1}{|x|\,{\sqrt {x^{2}-1}}}}}
Ekzemplo de pruvo: estu
θ
=
arcsin
x
{\displaystyle \theta =\arcsin x\!}
d
arcsin
x
d
x
=
d
θ
d
sin
θ
=
1
cos
θ
=
1
1
−
sin
2
θ
=
1
1
−
x
2
{\displaystyle {\frac {d\arcsin x}{dx}}={\frac {d\theta }{d\sin \theta }}={\frac {1}{\cos \theta }}={\frac {1}{\sqrt {1-\sin ^{2}\theta }}}={\frac {1}{\sqrt {1-x^{2}}}}}
Integraligo de la derivaĵo kaj fiksigo de la valoro je unu punkto donas esprimon por la inversa trigonometria funkcio kiel difinita integralo por reelaj valoroj de x :
arcsin
x
=
∫
0
x
1
1
−
z
2
d
z
,
|
x
|
≤
1
{\displaystyle \arcsin x=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,dz,\qquad |x|\leq 1}
arccos
x
=
∫
x
1
1
1
−
z
2
d
z
,
|
x
|
≤
1
{\displaystyle \arccos x=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,dz,\qquad |x|\leq 1}
arctan
x
=
∫
0
x
1
z
2
+
1
d
z
{\displaystyle \arctan x=\int _{0}^{x}{\frac {1}{z^{2}+1}}\,dz}
arccot
x
=
∫
x
∞
1
z
2
+
1
d
z
{\displaystyle \operatorname {arccot} x=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,dz}
arcsec
x
=
∫
1
x
1
z
z
2
−
1
d
z
,
x
≥
1
{\displaystyle \operatorname {arcsec} x=\int _{1}^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz,\qquad x\geq 1}
arccsc
x
=
∫
x
∞
1
z
z
2
−
1
d
z
,
x
≥
1
{\displaystyle \operatorname {arccsc} x=\int _{x}^{\infty }{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz,\qquad x\geq 1}
Se x=1 , la integraloj kun limigitaj domajnoj estas nepropraj integraloj , sed bone difinitaj.
Malderivaĵoj de inversaj trigonometriaj funkcioj [ redakti | redakti fonton ] Malderivaĵoj de inversaj trigonometriaj funkcioj por reelaj kaj kompleksaj argumentoj estas:
∫
arcsin
x
d
x
=
x
arcsin
x
+
1
−
x
2
+
C
{\displaystyle \int \arcsin x\,dx=x\,\arcsin x+{\sqrt {1-x^{2}}}+C}
∫
arccos
x
d
x
=
x
arccos
x
−
1
−
x
2
+
C
{\displaystyle \int \arccos x\,dx=x\,\arccos x-{\sqrt {1-x^{2}}}+C}
∫
arctan
x
d
x
=
x
arctan
x
−
1
2
ln
(
1
+
x
2
)
+
C
{\displaystyle \int \arctan x\,dx=x\,\arctan x-{\frac {1}{2}}\ln \left(1+x^{2}\right)+C}
∫
arccot
x
d
x
=
x
arccot
x
+
1
2
ln
(
1
+
x
2
)
+
C
{\displaystyle \int \operatorname {arccot} x\,dx=x\,\operatorname {arccot} x+{\frac {1}{2}}\ln \left(1+x^{2}\right)+C}
∫
arcsec
x
d
x
=
x
arcsec
x
−
ln
(
x
(
1
+
x
2
−
1
x
2
)
)
+
C
{\displaystyle \int \operatorname {arcsec} x\,dx=x\,\operatorname {arcsec} x-\ln \left(x\left(1+{\sqrt {\frac {x^{2}-1}{x^{2}}}}\right)\right)+C}
∫
arccsc
x
d
x
=
x
arccsc
x
+
ln
(
x
(
1
+
x
2
−
1
x
2
)
)
+
C
{\displaystyle \int \operatorname {arccsc} x\,dx=x\,\operatorname {arccsc} x+\ln \left(x\left(1+{\sqrt {\frac {x^{2}-1}{x^{2}}}}\right)\right)+C}
Por reelaj x≥1 :
∫
arcsec
x
d
x
=
x
arcsec
x
−
ln
(
x
+
x
2
−
1
)
+
C
{\displaystyle \int \operatorname {arcsec} x\,dx=x\,\operatorname {arcsec} x-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C}
∫
arccsc
x
d
x
=
x
arccsc
x
+
ln
(
x
+
x
2
−
1
)
+
C
{\displaystyle \int \operatorname {arccsc} x\,dx=x\,\operatorname {arccsc} x+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C}
Pro tio ke
∫
u
d
v
=
u
v
−
∫
v
d
u
{\displaystyle \int u\,\mathrm {d} v=uv-\int v\,\mathrm {d} u}
u
=
arcsin
x
d
v
=
d
x
d
u
=
d
x
1
−
x
2
v
=
x
{\displaystyle {\begin{aligned}u&{}=&\arcsin x&\quad \quad \mathrm {d} v=\mathrm {d} x\\\mathrm {d} u&{}=&{\frac {\mathrm {d} x}{\sqrt {1-x^{2}}}}&\quad \quad {}v=x\end{aligned}}}
Tiam
∫
arcsin
x
d
x
=
x
arcsin
x
−
∫
x
1
−
x
2
d
x
{\displaystyle \int \arcsin x\,\mathrm {d} x=x\arcsin x-\int {\frac {x}{\sqrt {1-x^{2}}}}\,\mathrm {d} x}
Integralado per anstataŭigo
k
=
1
−
x
2
{\displaystyle k=1-x^{2}\,}
d
k
=
−
2
x
d
x
{\displaystyle \mathrm {d} k=-2x\,\mathrm {d} x}
∫
x
1
−
x
2
d
x
=
−
1
2
∫
d
k
k
=
−
k
{\displaystyle \int {\frac {x}{\sqrt {1-x^{2}}}}\,\mathrm {d} x=-{\frac {1}{2}}\int {\frac {\mathrm {d} k}{\sqrt {k}}}=-{\sqrt {k}}}
Rea anstataŭigo de x liveras je:
∫
arcsin
x
d
x
=
x
arcsin
x
+
1
−
x
2
{\displaystyle \int \arcsin x\,\mathrm {d} x=x\arcsin x+{\sqrt {1-x^{2}}}}
La inversaj trigonometriaj funkcioj povas esti kalkulitaj per malfinia serio :
arcsin
z
=
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
=
∑
n
=
0
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
z
2
n
+
1
(
2
n
+
1
)
;
|
z
|
≤
1
{\displaystyle {\begin{aligned}\arcsin z&{}=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1\end{aligned}}}
arccos
z
=
π
2
−
arcsin
z
=
π
2
−
(
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
)
=
π
2
−
∑
n
=
0
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
z
2
n
+
1
(
2
n
+
1
)
;
|
z
|
≤
1
{\displaystyle {\begin{aligned}\arccos z&{}={\frac {\pi }{2}}-\arcsin z\\&{}={\frac {\pi }{2}}-\left(z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \right)\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1\end{aligned}}}
arctan
z
=
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
z
≠
i
,
−
i
{\displaystyle {\begin{aligned}\arctan z&{}=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}};\qquad |z|\leq 1\qquad z\neq i,-i\end{aligned}}}
arccot
z
=
π
2
−
arctan
z
=
π
2
−
(
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
)
=
π
2
−
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
z
≠
i
,
−
i
{\displaystyle {\begin{aligned}\operatorname {arccot} z&{}={\frac {\pi }{2}}-\arctan z\\&{}={\frac {\pi }{2}}-\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots \right)\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}};\qquad |z|\leq 1\qquad z\neq i,-i\end{aligned}}}
arcsec
z
=
arccos
(
z
−
1
)
=
π
2
−
(
z
−
1
+
(
1
2
)
z
−
3
3
+
(
1
⋅
3
2
⋅
4
)
z
−
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
−
7
7
+
⋯
)
=
π
2
−
∑
n
=
0
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
z
−
(
2
n
+
1
)
(
2
n
+
1
)
;
|
z
|
≥
1
{\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos(z^{-1})\\&{}={\frac {\pi }{2}}-\left(z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \right)\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{(2n+1)}};\qquad |z|\geq 1\end{aligned}}}
arccsc
z
=
arcsin
(
z
−
1
)
=
z
−
1
+
(
1
2
)
z
−
3
3
+
(
1
⋅
3
2
⋅
4
)
z
−
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
−
7
7
+
⋯
=
∑
n
=
0
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
z
−
(
2
n
+
1
)
2
n
+
1
;
|
z
|
≥
1
{\displaystyle {\begin{aligned}\operatorname {arccsc} z&{}=\arcsin(z^{-1})\\&{}=z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{2n+1}};\qquad |z|\geq 1\end{aligned}}}
Estas pli kompetenta serio por la tangentarko de Leonhard Euler :
arctan
x
=
x
1
+
x
2
∑
n
=
0
∞
∏
k
=
1
n
2
k
x
2
(
2
k
+
1
)
(
1
+
x
2
)
.
{\displaystyle \arctan x={\frac {x}{1+x^{2}}}\sum _{n=0}^{\infty }\prod _{k=1}^{n}{\frac {2kx^{2}}{(2k+1)(1+x^{2})}}.}
Rimarku ke la termo en la sumo por n=0 estas la malplena produto kiu estas 1.
Alternative, ĉi tio povas esti esprimita kiel:
arctan
x
=
∑
n
=
0
∞
2
2
n
(
n
!
)
2
(
2
n
+
1
)
!
x
2
n
+
1
(
1
+
x
2
)
n
+
1
{\displaystyle \arctan x=\sum _{n=0}^{\infty }{\frac {2^{\,2n}\,(n!)^{2}}{(2n+1)!}}\;{\frac {x^{\,2n+1}}{(1+x^{2})^{n+1}}}}
Alternativo al la potencoserio por tangentarko estas ĝia ĝeneraligita ĉenfrakcio :
arctan
(
z
)
=
z
1
+
z
2
3
+
4
z
2
5
+
9
z
2
7
+
16
z
2
9
+
25
z
2
⋱
{\displaystyle \arctan(z)={\cfrac {z}{1+{\cfrac {z^{2}}{3+{\cfrac {4z^{2}}{5+{\cfrac {9z^{2}}{7+{\cfrac {16z^{2}}{9+{\cfrac {25z^{2}}{\ddots \,}}}}}}}}}}}}\,}
Ĉi tio estas valida en la tranĉita kompleksa ebeno. Estas du tranĉoj, de -i al malfinio, suben laŭ la imaginara akso, kaj de i al malfinio supren laŭ la imaginara akso. Ĝiaj laboras plej bona por reelaj nombroj inter −1 kaj 1. La partaj denominatoroj estas la neparaj naturaj nombroj, kaj la partaj numeratoroj (post la unua) estas (nz)2 . Ĝi estis ellaborita de Carl Friedrich Gauss per la supergeometria serio .
Por kalkuli tangentarkon por x proksima al nulo, uzi la ĉenfrakcion pli supre.
Por kalkuli tangentarkon por aliaj valoroj de x :
arctan
x
=
2
arctan
x
1
+
1
+
x
2
.
{\displaystyle \arctan x=2\arctan {\frac {x}{1+{\sqrt {1+x^{2}}}}}.}
Por kalkuli sinusarkon:
arcsin
x
=
arctan
x
1
−
x
2
.
{\displaystyle \arcsin x=\arctan {\frac {x}{\sqrt {1-x^{2}}}}.}
Por kalkuli kosinusarkon:
arccos
x
=
π
2
−
arcsin
x
.
{\displaystyle \arccos x={\frac {\pi }{2}}-\arcsin x.}
Por kalkuli kotangentarkon:
arccot
x
=
π
2
−
arctan
x
.
{\displaystyle \operatorname {arccot} x={\frac {\pi }{2}}-\arctan x.}
Por kalkuli sekantarkon:
arcsec
x
=
π
2
−
arcsin
1
x
.
{\displaystyle \operatorname {arcsec} x={\frac {\pi }{2}}-\arcsin {\frac {1}{x}}.}
Por kalkuli kosekantarkon:
arccsc
x
=
arcsin
1
x
.
{\displaystyle \operatorname {arccsc} x=\arcsin {\frac {1}{x}}.}
La duargumenta funkcio atan2 komputas la tangentarkon de y/x por donitaj y kaj x , sed kun limigo de rezulto (-π,π]. Ĝi estis prezentita unua en multaj komputilaj programlingvoj sed estas komuna ankaŭ por scienco kaj inĝenierado.
Ĝi estas difinita per la funkcio arctan (kiu havas limigon de la rezulto (−π/2, π/2)):
atan2
(
y
,
x
)
=
{
arctan
(
y
x
)
x
>
0
π
+
arctan
(
y
x
)
y
≥
0
,
x
<
0
−
π
+
arctan
(
y
x
)
y
<
0
,
x
<
0
π
2
y
>
0
,
x
=
0
−
π
2
y
<
0
,
x
=
0
undefined
y
=
0
,
x
=
0
{\displaystyle \operatorname {atan2} (y,x)={\begin{cases}\arctan({\frac {y}{x}})&\qquad x>0\\\pi +\arctan({\frac {y}{x}})&\qquad y\geq 0,x<0\\-\pi +\arctan({\frac {y}{x}})&\qquad y<0,x<0\\{\frac {\pi }{2}}&\qquad y>0,x=0\\-{\frac {\pi }{2}}&\qquad y<0,x=0\\{\text{undefined}}&\qquad y=0,x=0\\\end{cases}}}
Ĉi tiu funkcio povas esti komputita per tangento de duona angulo :
atan2
(
y
,
x
)
=
2
arctan
y
x
2
+
y
2
+
x
{\displaystyle \operatorname {atan2} (y,x)=2\arctan {\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}}
se ĉu x > 0 aŭ y ≠ 0. Tamen, en praktika realiga pli bonas uzi la signojn de x kaj y por elekti la korektan rezulton.
La pli supre donita ordo de argumentoj (y, x) aspektas al esti la plej komuna, kaj en aparte estas uzata en la programlingvo C , sed kelkaj aŭtoroj povas uzi la kontraŭa konvencion (x, y). Ankaŭ, IEEE flosantaj punktaj realigoj devas kontroli esceptajn ne-nombrajn argumentajn valorojn.
La funkcio atan2 povas esti realigita en ciferece fidinda maniero per la maniero CORDIC .
Tial realigoj de atan(y) povas esti reale kiel atan2(y,1) .
Ĉi tiuj funkcioj povas ankaŭ esti esprimitaj per kompleksaj logaritmoj . Ĉi tiu etendas en natura maniero ilian domajnon al la kompleksa ebeno .
arcsin
x
=
−
i
log
(
i
x
+
1
−
x
2
)
=
arccsc
1
x
{\displaystyle \arcsin x=-i\,\log(i\,x+{\sqrt {1-x^{2}}})=\operatorname {arccsc} {\frac {1}{x}}}
arccos
x
=
−
i
log
(
x
+
x
2
−
1
)
=
π
2
+
i
log
(
i
x
+
1
−
x
2
)
=
π
2
−
arcsin
x
=
arcsec
1
x
{\displaystyle \arccos x=-i\,\log(x+{\sqrt {x^{2}-1}})={\frac {\pi }{2}}\,+i\log(i\,x+{\sqrt {1-x^{2}}})={\frac {\pi }{2}}-\arcsin x=\operatorname {arcsec} {\frac {1}{x}}}
arctan
x
=
i
2
(
log
(
1
−
i
x
)
−
log
(
1
+
i
x
)
)
=
arccot
1
x
{\displaystyle \arctan x={\frac {i}{2}}(\log(1-i\,x)-\log(1+i\,x))=\operatorname {arccot} {\frac {1}{x}}}
arccot
x
=
i
2
(
log
(
1
−
i
x
)
−
log
(
1
+
i
x
)
)
=
arctan
1
x
{\displaystyle \operatorname {arccot} x={\frac {i}{2}}\left(\log \left(1-{\frac {i}{x}}\right)-\log \left(1+{\frac {i}{x}}\right)\right)=\arctan {\frac {1}{x}}}
arcsec
x
=
−
i
log
(
1
x
2
−
1
+
1
x
)
=
i
log
(
1
−
1
x
2
+
i
x
)
+
π
2
=
π
2
−
arccsc
x
=
arccos
1
x
{\displaystyle \operatorname {arcsec} x=-i\,\log \left({\sqrt {{\frac {1}{x^{2}}}-1}}+{\frac {1}{x}}\right)=i\,\log \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)+{\frac {\pi }{2}}={\frac {\pi }{2}}-\operatorname {arccsc} x=\arccos {\frac {1}{x}}}
arccsc
x
=
−
i
log
(
1
−
1
x
2
+
i
x
)
=
arcsin
1
x
{\displaystyle \operatorname {arccsc} x=-i\,\log \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)=\arcsin {\frac {1}{x}}}
Ĉi tiuj formuloj sekvas de la trigonometriaj funkcioj per eksponenta funkcio , kiu veras por kompleksa argumento.
arcsin
x
=
θ
{\displaystyle \arcsin x\,=\,\theta }
e
i
θ
−
e
−
i
θ
2
i
=
x
{\displaystyle {\frac {e^{i\,\theta }-e^{-i\,\theta }}{2i}}\,=\,x}
Estu
k
=
e
i
θ
.
{\displaystyle k=e^{i\,\theta }.}
Tiam
k
−
1
k
2
i
=
x
{\displaystyle {\frac {k-{\frac {1}{k}}}{2i}}\,=\,x}
k
2
−
2
i
k
x
−
1
=
0
{\displaystyle k^{2}-2\,i\,k\,x-1\,=\,0}
k )
k
=
i
x
±
1
−
x
2
=
e
i
θ
{\displaystyle k\,=\,i\,x\pm {\sqrt {1-x^{2}}}\,=\,e^{i\,\theta }}
θ
=
arcsin
x
=
−
i
log
(
i
x
+
1
−
x
2
)
{\displaystyle \theta \,=\,\arcsin \,x\,=\,-i\log(i\,x+{\sqrt {1-x^{2}}})}
Orta triangulo ABC Inversaj trigonometriaj funkcioj estas utilaj por kalkuli angulojn de triangulo se estas sciataj longoj de lateroj de la triangulo, ekzemple per la leĝo de kosinusoj .
En orta triangulo , la funkcioj de rilatumoj de longoj de lateroj jam donas la angulon:
α = arcsin (a/c) = arccos (b/c) = arctan (a/b) = arccsc (c/a) = arcsec (c/b) = arccot (b/a)