Saltu al enhavo

Trigonometrio

Redakti ligilojn
El Vikipedio, la libera enciklopedio
Trigonometria cirklo montranta la sinuson kaj kosinuson

Trigonometrio (de greka trigonon – 'triangulo', metrô – 'mezuri') estas branĉo de matematiko, kiu studas triangulojn, angulojn, arkojn, kaj ilian interrilaton. Ĉi tiu interrilato estas esprimita uzante trigonometriajn funkciojn, la plej konataj el kiuj estas sinuso, kosinuso kaj tanĝanto. Ĝi studas ankaŭ trigonometriajn funkciojn kaj ilian aplikon en geometrio. Ekzistas ses trigonometriaj funkcioj ligitaj kun la angulo:

  • sinuso - la kvociento de la kontraŭa latero per la hipotenuzo (signo: sin). la difino povas estis etendita al ajna angulo per la formuloj:
;
;
;
,
kie estas orta angulo ( kaj ), kaj estas ajna angulo;
  • kosinuso (signo: cos) - sinuso de la komplementa angulo;
  • tangento (signo: tg aŭ tan) - la kvociento de la sinuso per la kosinuso;
  • kotangento (signo: ctg aŭ cot) - la kvociento de la kosinuso per la sinuso;
  • sekanto - la inverso de la kosinuso;
  • kosekanto - la inverso de la sinuso.

Laŭ trigonometriaj funkcio oni trovas nekonatajn angulojn kaj laterojn de triangulo surbaze de donitaj trigonometriaj rilatoj.

Oni kutime uzas la vorton trigonometrio por aludi al ebena trigonometrio, tio estas la studo de trianguloj sur ebena surfaco. Sed oni povas ankaŭ studi la rilatojn de trianguloj sur kurbaj surfacoj. Pro tio ke ni loĝas sur preskaŭ sfera surfaco, oni ankaŭ studas sferan trigonometrion, tio estas la studo de trianguloj sur sferaj surfacoj.

Trigonometrio formiĝis en la 3-a jarcento a.K. kiel branĉo de geometrio por uzoj en astronomio. Hodiaŭ trigonometrio havas multajn aplikojn preter astronomio, ekzemple por navigado, optiko kaj muzikteorio.

Trigonometriaj kalkulo kaj funkcioj

[redakti | redakti fonton]

Angulaj unuoj

[redakti | redakti fonton]

En la mezurado de anguloj kaj, tial, en trigonometrio, oni uzas tri unuojn, sed la plej uzita en la ĉiutaga vivo estas la angula grado; en matematiko estas la radiano la plej uzita, difinita kiel la natura unuo por mezuri angulojn; la centona grado disvolviĝis kiel unuo plej proksima al la dekuma sistemo, uzata en topografio, arkitekturo aŭ en konstruado.

  • Radiano (simbolo: rad): natura angula unuo en trigonometrio. En kompleta cirklo estas 2π radianoj (iom pli ol 6,28). Ĝi estas uzata ĉefe en trigonometrio kaj infinitezima kalkulo. Angulo inter du radiusoj de cirklo, arkolongo inter kiuj egalas al la radiuso, estas la ebena angulo.
  • Sesuma grado: angula unuo kiu dividas cirklon en 360 gradoj. Ĝi egalas al π / 180 radianoj, al naŭdekono de orto, aŭ al 10/9 gradusoj. La simbolo de grado estas °. Grado estas pli oportuna mezurunuo de angulo ol radiano, ĉar ĝi ebligas skribi multajn kutimajn angulojn (ekzemple orton) per entjera kvanto de gradoj. Por pli ĝusta mezuro de anguloj oni uzas aŭ dekumajn frakciojn de grado aŭ minutojn kaj sekundojn. Angula minuto estas 1/60 de grado. Angula sekundo estas 1/60 de angula minuto, do 1/3600 de grado. La simbolo de angula minuto estas ' kaj la simbolo de angula sekundo estas ".
  • Centuma grado: angula unuo kiu dividas cirklon en 400 centonaj gradoj. La graduso (mallongigo: gr) ankaŭ nomita gono (simbolo: gon, el la greka gônia = "angulo") estas egala al π / 200 radiano, al centono de orto, aŭ al 0,9 grado. Alimaniere priskribi estas ke la divido de la cirklo en 400 gradusoj, tiel ke en ĉiu rekta angulo estas 100 anguloj de gradusoj. La graduso estas la konsekvenco el la invento de la metro, ĉar la metro estas la 40.000.000-ono de la ter-ĉirkaŭo, kiam oni onigas tiun ĉirkaŭon per 400 gr, 1 km egalas al 1/100 da graduso. Pro tio, oni malbone komprenas ke oni ankoraŭ uzas la gradon en la aviadila kaj marveturada medioj kie la mezurunuoj estas la mar-mejlo (naŭta mejlo = 1854 metroj) kaj la deksesonaj unuoj.
  • Angula milo: angula unuo kiu dividas cirklon en 6 400 unuoj. Ĝi estas uzita en la milita medio, precipe en instrumentoj por orientigo kaj signalado. Ĝia simbolo estas "m" krucigita je 30 gradoj: .
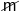Angulilo en radianoj Angulilo en sesumaj gradoj
Angulilo en centumaj gradoj Angulilo en angula milo

Trigonometriaj funkcioj

[redakti | redakti fonton]

En matematiko, la trigonometriaj funkcioj estas ses funkcioj de angulo.

Ili estas ekvivalente difinebla laŭ diversaj manieroj.

Por ke la geometriaj kaj la algebraj difinoj donu koincidantajn rezultojn, la angulo θ devas esti mezurita en radianoj.

La difino per orta triangulo senpere donas ĉiujn ses funkciojn. En iuj el la aliaj okazaj komence estas difinataj ne ĉiuj funkcioj (sin kaj cos tamen estas difinataj), la aliaj funkcioj estas tiam difinataj per formuloj de kolumno "Ĉefa idento" de la tabelo pli supre.

Skribmanieroj kaj grafikaĵoj

[redakti | redakti fonton]
Nomo Kutima skribmaniero Ĉefa idento Limigoj de valoro por reela argumento Periodo
sinuso y = sin θ −1 ≤ y ≤ 1 2π
kosinuso y = cos θ −1 ≤ y ≤ 1 2π
tangento y = tan θ aŭ
y = tg θ		 tan θ = sin θ / cos θ ĉiuj reelaj y π
kotangento y = cot θ aŭ
y = cotan θ aŭ
y = ctg θ		 cot θ = cos θ / sin θ ĉiuj reelaj y π
sekanto y = sec θ sec θ = 1 / cos θ −∞ < y ≤ −1 aŭ 1 ≤ y < ∞ 2π
kosekanto y = csc θ aŭ
y = cosec θ		 csc θ = 1 / sin θ −∞ < y ≤ −1 aŭ 1 ≤ y < ∞ 2π

Historio pri trigonometrio

[redakti | redakti fonton]

Jam de antikveco, trigonometrio estas uzata por celoj de astronomio.

Babilonia tabuleto Plimpton 322.

La antikvaj egiptanoj kaj babilonianoj konis la teoremojn pri la proporcioj de la flankoj de similaj trianguloj. Sed la prahelenaj socioj ne konis la nocion de mezuro de angulo kaj tial, la flankoj de la trianguloj estis studitaj nur pri ties mezuro, fako kiu povus esti nomita trilaterometrio.

La babiloniaj astronomoj faris registrojn pri la apero kaj malapero de la steloj, la movado de la planedoj kaj la suneklipsoj kaj luneklipsoj; ĉio tio postulas familiarecon kun la angula distanco mezurita sur la ĉiela sfero. Sur la bazo de la interpretado de kojnforme skribita tabuleto Plimpton 322 (ĉirkaŭ 1900 a.n.e.), kelkaj fakuloj asertis eĉ, ke la iamaj babilonianoj havis tabelon de sekantoj. Nuntempe, tamen, estas granda debato ĉu temas pri tabelo de pitagoraj triopoj, tabelo de solvoj de ekvacioj duagradaj aŭ eĉ trigonometria tabelo.

La antikvaj egiptanoj siavice, en la dua jarmilo antaŭ nia erao, uzis primitivan formon de trigonometrio, por la konstruado de la piramidoj. La Papiruso de Ahmes, verkita de la egipta skribisto Ahmes (ĉirkaŭ 1680-1620 a.n.e.), enhavas la jenan problemon rilatan al la trigonometrio:

Citaĵo
„ Se piramido esta 250 ulnojn alta kaj la latero de ties bazo estas 360 ulnojn longa, kiu estas ties seked? ”

[1] La solvo al la problemo estas la rilato inter la duono de la flanko de la bazo de la piramido kaj ĝia alteco. Alivorte, la mezuro trovebla por la seked estas la kotangento de la angulo kiun formas la bazo de la piramido kaj ĝia respektiva flanko.

Hiparko, konsiderata kiel kompilinto de la unua trigonometria tabelo, estis priskribita kiel "la patro de trigonometrio".[2]

En la 3-a jarcento a.n.e., helenismaj matematikistoj kiel Eŭklido kaj Arkimedo studis la proprecojn de kordoj kaj enskribitajn angulojn en cirkloj, kaj ili pruvis teoremojn kiuj estas ekvivalentaj al modernaj trigonometriaj formuloj, kvankam ili prezentis ilin geometrie anstataŭ algebre. En 140 a.n.e., Hiparko (de Niceo, Malgranda Azio) havigis la unuajn tabelojn de kordoj, analogajn al modernaj tabeloj de sinusvaloroj, kaj uzis ilin por solvi problemojn en trigonometrio kaj aparte en sfera trigonometrio.[3] En la 2-a jarcento n.e., la grek-egipta astronomo Ptolemeo (el Aleksandrio, Egiptio) konstruis detalajn trigonometriajn tabelojn (la tabelo de kordoj de Ptolemeo) en la Libro 1a, ĉapitro 11a de sia Almagesto.[4] Ptolemeo uzis kordolongon por difini siajn trigonometriajn funkciojn, kio estas negrava diferenco de la sinuskonvencio kiun oni uzas hodiaŭ.[5] (La valoro, kiun oni nomas sin(θ) troveblas, rigardante la kordlongon por duoble la angulo de intereso(2θ) en la tabelo de Ptolemeo, kaj poste dividante tiun valoron per du.) Jarcentoj pasis antaŭ ol pli detalaj tabeloj estis produktitaj, kaj la traktaĵo de Ptolemeo restis uzita por elfarado de trigonometriaj kalkuloj en astronomio dum la sekvaj 1200 jaroj en la mezepokaj bizancaj, islamaj, kaj poste okcidentaj mondoj.

La moderna difino de la sinuso unue estis asertita en la Surjo Siddhanta, kaj ĝiaj trajtoj estis plu dokumentitaj en la 5-a jarcento (n.e.) fare de la hinda matematikisto kaj astronomo Arĝabato.[6] Tiuj grekaj kaj hindaj verkoj estis tradukitaj kaj vastigitaj fare de mezepokaj islamaj matematikistoj. En 830 n.e., persa matematikisto Habaŝ al-Hasib al-Marŭazi produktis la unuan tabelon de kotangentoj.[7][8] Ĝis la 10-a jarcento n.e., en la laboro de persa matematikisto Abū al-Wafā' al-Būzjānī, ĉiuj ses trigonometriaj funkcioj estis uzitaj.[9] Abu al-Wafa havis sinusajn tabelojn en 0.25° pliigoj, al 8 decimalaj lokoj de precizeco, kaj precizajn tabelojn de tanĝantaj valoroj.[9] Li ankaŭ faris gravajn inventojn en sfera trigonometrio.[10][11][12]

Nasir al-Din al-Tusi

La persa polimato Nasir al-Din al-Tusi estis priskribita kiel la kreinto de trigonometrio kiel matematika fako per si mem.[13][14][15] Li estis la unua, kiu traktis trigonometrion kiel matematika fako sendependa el astronomio, kaj li disvolvis sferan trigonometrion kia ĝi estas en nuntempa formo.[8] Li listigis la ses malsamajn kazojn de ortangula triangulo en sfera trigonometrio, kaj en sia Pri la Sektorfiguro, li asertis, ke la leĝo de sinusoj por ebenaj kaj sferaj trianguloj, malkovris la Leĝon de tangentoj por sferaj trianguloj, kaj havigis pruvojn por tiuj ambaŭ leĝoj.[16] Sciaro pri trigonometriaj funkcioj kaj metodoj atingis Okcidentan Eŭropon tra latinlingvaj tradukoj de la greklingva verko de Ptolemeo Almagesto same kiel la verkoj de persaj kaj arabaj astronomoj kiel Al Battani kaj Nasir al-Din al-Tusi.[17] Unu el la plej fruaj verkoj pri trigonometrio fare de nordeŭropa matematikisto estas De Triangulis de la 15a-jarcenta germana matematikisto Regiomontanus, kiun kuraĝis verki, kaj eĉ disponigis ekzempleron de la Almagesto, la bizanca greklingva fakulo kardinalo Basilios Bessarion kun kiu li loĝis kelkajn jarojn.[18] Samtempe, alia traduko de la Almagesto el la greka al Latino estis kompletigita de la kreta Georgo de Trebizondo.[19] Trigonometrio estis ankoraŭ malmulte konata en la 16-a jarcento en norda Eŭropo kiam Nicolaus Copernicus dediĉis du ĉapitrojn de De revolutionibus orbium coelestium por klarigi sian bazajn konceptojn.

Movita de la postuloj de navigacio kaj la kreskanta bezono de precizaj mapoj de grandaj geografiaj areoj, trigonometrio kreskis en gravan branĉon de matematiko.[20] Bartolomeo Pitisko estis la unua, kiu uzis la vorton, publikigante sian Trigonometria en 1595.[21] Gemma Frisius priskribis por la unua fojo la metodon de triangulado ankoraŭ uzata hodiaŭ en geodezio. Estis Leonhard Euler kiu plene integrigis kompleksajn nombrojn en trigonometrio. La verkoj de la skotaj matematikistoj James Gregory en la 17-a jarcento kaj Colin Maclaurin en la 18-a jarcento estis influaj en la evoluo de trigonometriaj serioj. [22] Ankaŭ en la 18-a jarcento, Brook Taylor difinis la ĝeneralan Taylor-serion.[23]

Racionala trigonometrio

[redakti | redakti fonton]

Racionala trigonometrio estas moderna traktado de trigonometrio uzanta la konceptojn etendeco-n kaj kvadranco-n anstataŭ angulon kaj distancon. Anstataŭ la klasikaj funkcioj (sinuso, kosinuso, tangento) ĝi uzas nur algebrajn operaciojn. Tiu nova maniero estas la laboro de Doktoro Norman Wildberger de la Universitato de Nova Sud-Kimrio (ĉe Sidnejo en Aŭstralio). Pli da informo estas havebla je lia paĝaro [1]. Ĝia nomo devenas de la malplia uzado de neracionalaj nombroj, kiel kvadratoradikoj kaj la matematika konstanto π kiu estas neracionala.

Kvadranco - la apartiĝo inter punktoj

[redakti | redakti fonton]

Kvadranco ("") diferencas ol simpla distanco ĉar ĝi kvadratigas la distancon. Ĉi tio signifas ke oni povas plifacile kalkuli la apartiĝon inter du punktoj en 2-dimensia spaco, ĉar oni ne devas trovi la kvadratoradikon, kiu ofte estas neracionala.

En kartezia spaco , inter la punktoj kaj , la kvadranco estas difinita kiel,

Etendeco - la apartiĝo inter linioj

[redakti | redakti fonton]

Laŭ racionala trigonometrio, etendeco ("") estas fundamenta koncepto difinita kiel la proporcio de du kvadrancoj. Establu punkto kie du linioj kruciĝas, kaj elektu du punktojn sur unu kaj sur la alia tiel, kiel la linio estas orta laŭ .

Inter la linioj kaj , la etendeco estas difinita kiel,

Aplikoj

[redakti | redakti fonton]

Astronomio

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikolo Astronomio.

Dum jarcentoj, oni uzis sferaj trigonometrion por lokigi sunajn, lunajn kaj stelajn poziciojn,[24] antaŭvidante eklipsojn, kaj priskribante la orbitojn de planedoj.[25]

En nuntempa epoko, la tekniko de triangulado estas uzata en astronomio por mezuri la distancon de proksimaj steloj,[26] same kiel por Terglobnavigadaj satelitsistemoj.[12]

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikolo Navigacio.
Sekstantoj estas uzataj por mezuri la angulon de la suno aŭ de steloj rilate al la horizonto. Uzante trigonometrion kaj markronometron, la pozicion de la ŝipo povas esti determinata pere de tiaj mezuroj.

Historie, trigonometrio estis uzita por lokalizi latitudojn kaj longitudojn de velŝipoj, plani kursojn, kaj kalkuli distancojn dum navigado.[27]

Trigonometrio estas ankoraŭ uzata en navigacio pere de rimedoj kiel la Tutmonda loktrova sistemo kaj artefarita inteligento por aŭtonomaj vehikloj.[28]

Termezurado

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikolo Termezurado.

En termezurado, trigonometrio estas uzata en la kalkulado de longoj, areoj kaj relativaj anguloj inter objektoj.[29]

Je pli granda skalo, trigonometrio estas uzata en geografio por mezuri distancojn inter termarkoj.[30]

Periodaj funkcioj

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikoloj Vico de Fourier kaj Furiera transformo.
Funkcio (en ruĝa) estas sumo de ses sinusaj funkcioj de malsamaj amplitudoj kaj harmonie rilataj frekvencoj. Ilia sumo estas nomita Fourier-serio. La transformo de Fourier, (en blua), kiu prezentas amplitudon kontraŭ frekvenco, rivelas la 6 frekvencojn (ĉe neparaj harmonoj) kaj iliajn amplitudojn (1/nepara nombro).

La sinusaj kaj kosinusaj funkcioj estas fundamentaj al la teorio de periodaj funkcioj,[31] kiel tiuj kiuj priskribas sonajn kaj lumajn ondojn. Fourier malkovris, ke ĉiu kontinua, perioda funkcio povus esti priskribita kiel senfina sumo de trigonometriaj funkcioj.

Eĉ ne-periodaj funkcioj povas esti reprezentataj kiel integralo de sinusoj kaj kosinusoj pere de la Furiera transformo. Tio ebligas aplikojn por kvantuma mekaniko[32] kaj komunikoj,[33] among other fields.

Optiko kaj akustiko

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikoloj Optiko kaj akustiko.

Trigonometrio estas utila en multaj fizikaj sciencoj,[34] kiel akustiko,[35] kaj optiko.[35] En ĉi tiuj areoj, ili estas uzataj por priskribi sonajn kaj lumajn ondojn, kaj por solvi lim- kaj dissend-rilatajn problemojn.[36]

Aliaj aplikoj

[redakti | redakti fonton]

Aliaj fakoj kiuj uzas trigonometrion aŭ trigonometriajn funkciojn estas muzikteorio,[37] geodezio, aŭdiosintezo,[38] arkitekturo,[39] elektroniko,[37] biologio,[40] medicina bildigo (komputila tomografio kaj ultrasono),[41] kemio,[42] nombroteorio (kaj de tie kriptologio),[43] sismologio,[35] meteologio,[44] oceanografio,[45] bildokunpremado,[46] fonetiko,[47] ekonomiko,[48] elektra inĝenierado, mekanika inĝenierado, civila inĝenierado,[37] komputila grafiko,[49] kartografio,[37] kristalografio[50] kaj videoludoj.[49]

Vidu ankaŭ

[redakti | redakti fonton]

Notoj

[redakti | redakti fonton]
  1. ↑ Seked estis iama egipta mezurunuo por la klino de la triangulaj flankoj de rekta piramido.
  2. ↑ Boyer (1991), p. 162, "Greek Trigonometry and Mensuration".
  3. ↑ Thurston (1996), pp. 235–236, "Appendix 1: Hipparchus's Table of Chords".
  4. ↑ Toomer, G. (1998), Ptolemy's Almagest, Princeton University Press, (ISBN 978-0-691-00260-6) 
  5. ↑ Thurston (1996), pp. 239–243, "Appendix 3: Ptolemy's Table of Chords".
  6. ↑ Boyer (1991), p. 215.
  7. ↑ Jacques Sesiano. (2000) “Islamic mathematics”, Mathematics Across Cultures: The History of Non-western Mathematics. Springer Science+Business Media. ISBN 978-1-4020-0260-1.
  8. ↑ 8,0 8,1 trigonometry. Encyclopædia Britannica. Alirita 2008-07-21 .
  9. ↑ 9,0 9,1 Boyer 1991, p. 238.
  10. ↑ (2011) “Mathematical Methods in Abū al-Wafāʾ's Almagest and the Qibla Determinations”, Arabic Sciences and Philosophy 21 (1), p. 1–56. doi:10.1017/S095742391000007X. 171015175. 
  11. ↑ Gingerich, Owen. "Islamic astronomy." Scientific American 254.4 (1986): 74–83
  12. ↑ 12,0 12,1 Michael Willers. (13a de Februaro 2018) Armchair Algebra: Everything You Need to Know From Integers To Equations. Book Sales. ISBN 978-0-7858-3595-0.
  13. ↑ Nasir al-Din al-Tusi. Alirita 2021-01-08 . “One of al-Tusi's most important mathematical contributions was the creation of trigonometry as a mathematical discipline in its own right rather than as just a tool for astronomical applications. In Treatise on the quadrilateral al-Tusi gave the first extant exposition of the whole system of plane and spherical trigonometry. This work is really the first in history on trigonometry as an independent branch of pure mathematics and the first in which all six cases for a right-angled spherical triangle are set forth.”.
  14. ↑ Berggren, J. L.. (October 2013) “Islamic Mathematics”, the cambridge history of science 2. Cambridge University Press, p. 62–83. doi:10.1017/CHO9780511974007.004. ISBN 9780521594486.
  15. ↑ “ṬUSI, NAṢIR-AL-DIN i. Biography”, Encyclopaedia Iranica.
  16. ↑ Berggren, J. Lennart. (2007) “Mathematics in Medieval Islam”, The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. ISBN 978-0-691-11485-9.
  17. ↑ Boyer, 1991, pp. 237, 274
  18. ↑ Johann Müller Regiomontanus. Alirita 2021-01-08 .
  19. ↑ N.G. Wilson (1992). From Byzantium to Italy. Greek Studies in the Italian Renaissance, London. ISBN 0-7156-2418-0
  20. ↑ Grattan-Guinness, Ivor. (1997) The Rainbow of Mathematics: A History of the Mathematical Sciences. W.W. Norton. ISBN 978-0-393-32030-5.
  21. ↑ Robert E. Krebs. (2004) Groundbreaking Scientific Experiments, Inventions, and Discoveries of the Middle Ages and the Renaissance. Greenwood Publishing Group. ISBN 978-0-313-32433-8.
  22. ↑ Ewald, William Bragg. (2005-04-21) From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics (angle). OUP Oxford. ISBN 978-0-19-152309-0.
  23. ↑ Dempski, Kelly. (Novembro 2002) Focus on Curves and Surfaces (angle). Premier Press. ISBN 978-1-59200-007-4.
  24. ↑ Olinthus Gregory. (1816) Elements of Plane and Spherical Trigonometry: With Their Applications to Heights and Distances Projections of the Sphere, Dialling, Astronomy, the Solution of Equations, and Geodesic Operations. Baldwin, Cradock, and Joy.
  25. ↑ (1948) “Mathematical methods in ancient astronomy”, Bulletin of the American Mathematical Society 54 (11), p. 1013–1041. doi:10.1090/S0002-9904-1948-09089-9. 
  26. ↑ (5a de Januaro 2009) Astronomy: The Solar System and Beyond. Cengage Learning. ISBN 978-0-495-56203-0.
  27. ↑ John Sabine. (1800) The Practical Mathematician, Containing Logarithms, Geometry, Trigonometry, Mensuration, Algebra, Navigation, Spherics and Natural Philosophy, Etc.
  28. ↑ (2018) Elements of Robotics. Springer. ISBN 978-3-319-62533-1.
  29. ↑ George Roberts Perkins. (1853) Plane Trigonometry and Its Application to Mensuration and Land Surveying: Accompanied with All the Necessary Logarithmic and Trigonometric Tables. D. Appleton & Company.
  30. ↑ (14 December 2015) Geographers: Biobibliographical Studies. A&C Black. ISBN 978-1-4411-0785-5.
  31. ↑ (7a de Aŭgusto 2003) Fourier and Laplace Transforms. Cambridge University Press. ISBN 978-0-521-53441-3.
  32. ↑ Bernd Thaller. (8a de Majo 2007) Visual Quantum Mechanics: Selected Topics with Computer-Generated Animations of Quantum-Mechanical Phenomena. Springer Science & Business Media. ISBN 978-0-387-22770-2.
  33. ↑ M. Rahman. (2011) Applications of Fourier Transforms to Generalized Functions. WIT Press. ISBN 978-1-84564-564-9.
  34. ↑ (1966) Trigonometry for the Physical Sciences. Appleton-Century-Crofts.
  35. ↑ 35,0 35,1 35,2 (1988) College Algebra and Trigonometry: Basics Through Precalculus. Scott, Foresman. ISBN 978-0-673-18393-4.
  36. ↑ Dudley H. Towne. (5 May 2014) Wave Phenomena. Dover Publications. ISBN 978-0-486-14515-0.
  37. ↑ 37,0 37,1 37,2 37,3 (1 November 1992) Plane Trigonometry. McGraw-Hill. ISBN 978-0-07-028187-5.
  38. ↑ (18a de Aprilo 2006) Applications of Digital Signal Processing to Audio and Acoustics. Springer Science & Business Media. ISBN 978-0-306-47042-4.
  39. ↑ (9a de Februaro 2015) Architecture and Mathematics from Antiquity to the Future: Volume I: Antiquity to the 1500s. Birkhäuser. ISBN 978-3-319-00137-1.
  40. ↑ Dan Foulder. (15a de Julio 2019) Essential Skills for GCSE Biology. Hodder Education. ISBN 978-1-5104-6003-4.
  41. ↑ (1995) Medical Imaging: Analysis of Multimodality 2D/3D Images. IOS Press. ISBN 978-90-5199-210-6.
  42. ↑ Marcus Frederick Charles Ladd. (2014) Symmetry of Crystals and Molecules. Oxford University Press. ISBN 978-0-19-967088-8.
  43. ↑ (22a de Aŭgusto 2008) Trigonometric Sums in Number Theory and Analysis. Walter de Gruyter. ISBN 978-3-11-019798-3.
  44. ↑ (1943) Study Guide for the Course in Meteorological Mathematics: Latest Revision, Feb. 1, 1943.
  45. ↑ (1980) Oceanography, the past. Springer-Verlag. ISBN 978-0-387-90497-9.
  46. ↑ JPEG Standard (JPEG ISO/IEC 10918-1 ITU-T Recommendation T.81). International Telecommunication Union (1993). Alirita 6a de Aprilo 2019 .
  47. ↑ Kirsten Malmkjaer. (4a de Decembro 2009) The Routledge Linguistics Encyclopedia. Routledge. ISBN 978-1-134-10371-3.
  48. ↑ Kamran Dadkhah. (11 January 2011) Foundations of Mathematical and Computational Economics. Springer Science & Business Media. ISBN 978-3-642-13748-8.
  49. ↑ 49,0 49,1 Christopher Griffith. (12a de Novembro 2012) Real-World Flash Game Development: How to Follow Best Practices AND Keep Your Sanity. CRC Press. ISBN 978-1-136-13702-0.
  50. ↑ John Joseph Griffin. (1841) A System of Crystallography, with Its Application to Mineralogy. R. Griffin.

Bibliografio

[redakti | redakti fonton]

Eksteraj ligiloj

[redakti | redakti fonton]
Bibliotekoj
Elŝutita el "https://eo.wikipedia.org/w/index.php?title=Trigonometrio&oldid=9176112"