Funkcio de eraro

Grafikaĵo de funkcio de eraro (erf)

Grafikaĵo de komplementa funkcio de eraro (erfc)

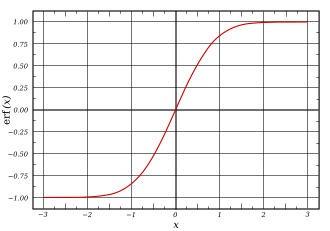
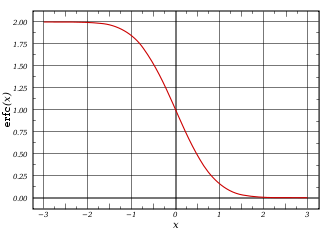
Funkcio de eraro de Gauss — ne fundamenta funkcio, kiu estas en probablokalkulo, statistiko kaj en teorio de parta diferenciala ekvacio. Ĝi estas difinita kiel:

$\text{erf}\left(x\right)={2\over\sqrt{\pi}}\int_0^xe^{-t^2}\,\mathrm dt$

Funkcio $\text{erf}$ estas strikte kunigita kun koopta funkcio de eraro $\text{erfc}$:

$\text{erfc}\left(x\right)$	$\equiv1-\text{erf}\left(x\right)$
	$={2\over\sqrt\pi}\int_x^\infty e^{-t^2}\,\mathrm dt$

Oni povas difini ankaŭ kompleksan funkcion de eraro $w\left(x\right)$, ĝi estas ankaŭ nomata kiel funkcio de Faddeeva:

$w(x)=e^{-x^2}\text{erfc}\left(-ix\right)$

Ecoj

• Funkcio de eraro estas malpara: $\text{erf}\left(z\right)=-\text{erf}\left(-z\right)$
• Kompleksa konjugito de argumento kauzas kompleksa konjugito de funkcio: $\text{erf}\left(z^*\right)=\left(\text{erf}\left(z\right)\right)^*$
• Por entjeroj funkcio havas limesojn kiel sube:

  $\text{erf}\left(\pm\infty\right)=\pm1$

• Por imaginara:

  $\text{erf}\left(\pm i\infty\right)=\pm i\infty$

• Derivaĵo kaj malderivaĵo de funkcio de eraro estas forte ligita kun normala distribuo:

  ${d\over dz}\text{erf}\left(z\right)={2\over\sqrt\pi}e^{-z^2}$

  $F\left(z\right)=z\,\text{erf}\left(z\right)+{e^{-z^2}\over\sqrt\pi}$

Serio de Taylor

La funkcio de eraro povas esprimi kiel disvolvo en serio de Taylor:

$\text{erf}\left(x\right) = \frac{2}{\sqrt{\pi}}\sum_{n=0}^\infin\frac{(-1)^n x^{2n+1}}{(2n+1)n!}=\frac{2}{\sqrt{\pi}} \left(x-\frac{x^3}{3}+\frac{x^5}{10}-\frac{x^7}{42}+\frac{x^9}{216}-\ \cdots\right)$

por ĉiu reala x.

Por $|x|\ll1$, valoro de funkcio de eraro povas facile kalkuli uzante:

$\text{erf}\left(x\right) ={2\over\sqrt\pi}e^{-x^2}\sum_{n=0}^\infty{2^n\over\left(2n+1\right)!!}x^{2n+1} ={2\over\sqrt\pi}e^{-x^2}\left(x+{2x^3\over1\cdot3}+{4x^5\over1\cdot3\cdot5}+{8x^7\over1\cdot3\cdot5\cdot7}+\cdots\right)$

kaj k!! signifas Duopa faktorialo de k.

Por $|x|\gg1$, facila estas suba disvolvo:

$\text{erf}\left(x\right) =1-{e^{-x^2}\over\sqrt\pi}\sum_{n=0}^\infty{(-1)^n(2n-1)!!\over2^n}x^{-2n-1)} =1-{e^{-x^2}\over\sqrt\pi}\left({1\over x}-{1\over2x^3}+{1\cdot3\over4x^5}-{1\cdot3\cdot5\over8x^7}+\cdots\right)$

Tabelo de valoroj

x	erf(x)	erfc(x)		x	erf(x)	erfc(x)
0.00	0.0000000	1.0000000		1.30	0.9340079	0.0659921
0.05	0.0563720	0.9436280		1.40	0.9522851	0.0477149
0.10	0.1124629	0.8875371		1.50	0.9661051	0.0338949
0.15	0.1679960	0.8320040		1.60	0.9763484	0.0236516
0.20	0.2227026	0.7772974		1.70	0.9837905	0.0162095
0.25	0.2763264	0.7236736		1.80	0.9890905	0.0109095
0.30	0.3286268	0.6713732		1.90	0.9927904	0.0072096
0.35	0.3793821	0.6206179		2.00	0.9953223	0.0046777
0.40	0.4283924	0.5716076		2.10	0.9970205	0.0029795
0.45	0.4754817	0.5245183		2.20	0.9981372	0.0018628
0.50	0.5204999	0.4795001		2.30	0.9988568	0.0011432
0.55	0.5633234	0.4366766		2.40	0.9993115	0.0006885
0.60	0.6038561	0.3961439		2.50	0.9995930	0.0004070
0.65	0.6420293	0.3579707		2.60	0.9997640	0.0002360
0.70	0.6778012	0.3221988		2.70	0.9998657	0.0001343
0.75	0.7111556	0.2888444		2.80	0.9999250	0.0000750
0.80	0.7421010	0.2578990		2.90	0.9999589	0.0000411
0.85	0.7706681	0.2293319		3.0	0.9999779	0.0000221
0.90	0.7969082	0.2030918		3.10	0.9999884	0.0000116
0.95	0.8208908	0.1791092		3.20	0.9999940	0.0000060
1.00	0.8427008	0.1572992		3.30	0.9999969	0.0000031
1.10	0.8802051	0.1197949		3.40	0.9999985	0.0000015
1.20	0.9103140	0.0896860		3.50	0.9999993	0.0000007

Referencoj

• Milton Abramowitz-a kaj Ireno A. Stegun, eds. Gvidlibro de Matematikaj Funkcioj kun Formuloj, Grafikaĵoj, kaj Matematikaj Tabeloj. (Novjorko): Dovero, 1972. (Vidi Ĉapitro 7)

Eksteraj ligiloj

• MathWorld-Erf