Hiperkubo



En geometrio, hiperkubo estas n-dimensia regula hiperpluredro, analogo de kvadrato (n = 2) kaj kubo (n = 3). Ĝi estas fermita, kompakta, konveksa figuro kies 1-skeleto konsistas el grupoj de kontraŭaj paralelaj strekoj laŭliniigita en ĉiu el la spacaj dimensioj, orte unu al la alia.
n-dimensia hiperkubo iamestas ankaŭ nomata kiel n-kubo.
La hiperkubo estas la speciala okazo de hiperortangulo.
Unuobla hiperkubo estas hiperkubo kies flanko havas longon 1. Ofte, la hiperkubo kies verticoj estas la 2n punktoj en Rn kun koordinatoj egalaj al 0 aŭ 1 estas nomata kiel "la" unuobla hiperkubo.
Punkto estas 0-hiperkubo. Se movi ĉi tiun punkto je distanco 1 ĝi balaas strekon kiu estas 1-hiperkubo de dimensio 1. Se movi ĉi tiun strekon perpendikulare al ĝi je distanco 1 ĝi balaas 2-dimensian kvadraton kiu estas 2-hiperkubo. Se movis la kvadraton perpendikulare al ĝia ebeno je distanco 1 ĝi balaas 3-dimensian kubon kiu estas 3-hiperkubo. Se movi kubon perpendikulare al ĝia 3-spaco ĝi balaas 4-dimensian 4-hiperkubon.
Rilatantaj familioj de hiperpluredroj[redakti | redakti fonton]
Hiperkuboj estas unu el la tri familioj de regulaj hiperpluredroj kiuj ekzistas en spacoj de ĉiu dimensio.
La aliaj du familioj estas la kruco-hiperpluredroj kaj la simplaĵoj. La kvara familio estas la malfiniaj hiperkubaj kahelaroj.
La duala hiperpluredro de n-hiperkubo estas n-kruco-hiperpluredro.
Alia rilatanta familio de uniformaj hiperpluredroj estas la duonverticaj hiperkuboj kiuj estas konstruitaj de hiperkuboj per alternado, do per forigo de duono de la verticoj kaj anstataŭigo ilin per (n-1)-simplaĵaj facetoj.
Eroj[redakti | redakti fonton]
Hiperkubo de dimensio n havas 2n flankoj. 1-dimensia streko havas 2 finaj punktoj; 2-dimensia kvadrato havas 4 laterojn; 3-dimensia kubo havas 6 2-dimensiaj edroj; 4-dimensia 4-hiperkubo havas 8 3-dimensiajn ĉeloj.
La kvanto de m-hiperkuboj eb la rando de n-hiperkubo estas
Tiel, la kvanto de verticoj de n-hiperkubo estas 2n.
Ekzemple, la rando de 4-hiperkubo enhavas 8 kuboj, 24 kvadratoj, 32 strekojn kaj 16 verticoj.
| Dimensio | Nomo | Grafeo | Simbolo de Schläfli Figuro de Coxeter-Dynkin |
Verticoj | Lateroj | Edroj | Ĉeloj | 4-hiperedroj | 5-hiperedroj | 6-hiperedroj | 7-hiperedroj | 8-hiperedroj |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Punkto | 
|
- | 1 | ||||||||
| 1 | Streko | 
|
{} |
2 | 1 | |||||||
| 2 (plurlatero) | Kvadrato | 
|
{4} |
4 | 4 | 1 | ||||||
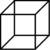
| 3 (pluredro) | Kubo (sesedro) |
|
{4,3} |
8 | 12 | 6 | 1 | |||||
| 4 (plurĉelo) | 4-hiperkubo (8-ĉelo) |

|
{4,3,3} |
16 | 32 | 24 | 8 | 1 | ||||
| 5 | 5-hiperkubo | 
|
{4,3,3,3} |
32 | 80 | 80 | 40 | 10 | 1 | |||
| 6 | 6-hiperkubo | 
|
{4,3,3,3,3} |
64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7 | 7-hiperkubo | 
|
{4,3,3,3,3,3} |
128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8 | 8-hiperkubo | 
|
{4,3,3,3,3,3,3} |
256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9 | 9-hiperkubo | 
|
{4,3,3,3,3,3,3,3} |
512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Vidu ankaŭ[redakti | redakti fonton]
- Familioj de diversdimensiaj hiperpluredroj kaj kahelaroj:
- Listo de regulaj hiperpluredroj
Referencoj[redakti | redakti fonton]
- Bowen, J. P., Hiperkuboj, Praktika komputa, 5(4):97–99, aprilo 1982 Arkivigite je 2008-06-30 per la retarkivo Wayback Machine.
- H. S. M. Coxeter, Regular Polytopes - Regulaj hiperpluredroj, 3-a. red., Dover Publications, 1973. ISBN 0-486-61480-8. (p. 296, Tabelo I (iii): Regulaj hiperpluredroj, tri regulaj hiperpluredroj en n dimensioj (n ≥ 5))
Eksteraj ligiloj[redakti | redakti fonton]
- Eric W. Weisstein, Hiperkubo en MathWorld.
- George Olshevsky, Mezura hiperpluredro en Glossary for Hyperspace.
- Hiperkubaj bildoj Arkivigite je 2007-09-26 per la retarkivo Wayback Machine (2D–15D)
- Animacio de hiperkubo


