Konveksa unuforma kahelaro de eŭklida 3-spaco
En geometrio, konveksa unuforma kahelaro de eŭklida 3-spaco estas unuforma kahelaro de tri-dimensia eŭklida spaco kun ne-interkovrantaj konveksaj unuformaj pluredraj ĉeloj. Vorto konveksa ĉi tie ne estas uzata plene laŭ difino de la konveksa aro, sed analoge al kondiĉoj de konvekseco de hiperpluredro. Do, konveksa kahelaro estas kahelaro kiu verigas kondiĉojn de konvekseco de hiperpluredro, krom tio ke la angula difekto ne estas pozitiva.
Ekzistas 28 ĉi tiaj kahelaroj:
- La sola regula kahelaro de eŭklida 3-spaco, kuba kahelaro, kaj 7 ĝiaj tranĉoj;
- La alternita kuba kahelaro kaj 4 ĝiaj tranĉoj;
- 10 prismaj formoj bazitaj je la unuformaj ebenaj kahelaroj (la 11-a el ili estas jam listigita kuba kahelaro);
- 5 ŝanĝoj de iuj el la pli supre listigitaj per plilongigo aŭ turnigo.
Ili povas esti konsiderataj la tri-dimensiaj analogoj de la unuformaj kahelaroj de la ebeno.
Historio
[redakti | redakti fonton]- 1900: Thorold Gosset skribis liston de duonregulaj konveksaj hiperpluredroj kun regulaj ĉeloj (platonaj solidoj) en sia eldono Pri la regula kaj duonregula figuroj en spaco de n dimensioj, inkluzivante unu regulan kuban kahelaron kaj du duonregulajn formojn kun kvaredroj kaj okedroj.
- 1905: Alfredo Andreini listigis na 25 el ĉi tiuj kahelaroj.
- 1991: Norman Johnson en manuskripto Unuformaj hiperpluredroj listigis la ĉiuj 28.
- 1994: Branko Grünbaum, en sia papero Unuformaj kahelaroj de 3-spaco sendepende listigis la ĉiuj 28, post malkovro de eraroj en eldono de Andreini. Li trovis ke en la papero de Andreini 1 kahelaro estas erara, kaj 4 turnitaj kaj plilongigitaj formoj forestas. Grünbaum ankaŭ skribis ke I. Aleksejev de Rusio ankaŭ sendepende listigis ĉi tiujn formojn proksimume en la sama tempo.
- 2006: George Olshevsky en sia manuskripto elvolvas plu derivitan liston de 143 konveksaj unuformaj kahelaroj de 4-spaco.
Nur 14 de la konveksaj unuformaj pluredroj aperi en ĉi tiuj ŝablonoj:
- 3 el la 5 platonaj solidoj - kvaredro, okedro, kubo;
- 6 el la 13 arĥimedaj solidoj - senpintigita kvaredro, kubokedro, senpintigita okedro, senpintigita kubo, malgranda rombokub-okedro, granda rombokub-okedro;
- 4 el la malfinia familio de prismoj - triangula prismo, seslatera prismo, oklatera prismo, dekdulatera prismo (ne listigante ĉi tie kubon).
Indeksoj
[redakti | redakti fonton]Por referencoj, ĉi tie estas donitaj indeksoj de la kahelaroj laŭ la laboroj de:
- A - Andreini (1-22)
- W - Williams (1-2,9-19)
- J - Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65)
- G - Grünbaum (1-28)
Ĉi tiuj kahelaroj iam estas nomataj kiel kahelaroj de Andreini.
Kahelaroj listigitaj laŭ malfiniaj grupoj de Coxeter
[redakti | redakti fonton]
Lateroj estas kolorigitaj per iliaj reflektaj ordoj:
ruĝa - ordo 2
verda - ordo 3
malhela blua - ordo 4.
R4 enspacas na 1/24 de la kubo. S4 enspacas na 1/12 de la kubo. P4 enspacas na 1/6 de la kubo.
La fundamentaj malfiniaj grupoj de Coxeter por eŭklida 3-spaco estas:
- R4, [4,3,4], kuba,






 (8 unikaj formoj, la alternita formo respektivas al la sekva alineo)
(8 unikaj formoj, la alternita formo respektivas al la sekva alineo) - S4, h[4,3,4], alternita kuba,




 (11 formoj, 4 novaj)
(11 formoj, 4 novaj) - P4 cikla grupo,


 (5 formoj, 1 nova)
(5 formoj, 1 nova)
La prismaj kolonoj de malfiniaj grupoj de Coxeter por eŭklida 3-spaco estas:
- R3xW2, [4,4]x[∞] prisma grupo,








 (2 novaj formoj)
(2 novaj formoj) - V3xW2, [6,3]x[∞] prisma grupo,








 (7 novaj formoj)
(7 novaj formoj) - P3xW2, [Δ]x[∞] prisma grupo,



 (sen novaj formoj)
(sen novaj formoj) - W2xW2xW2, [∞]x[∞]x[∞] prisma grupo,










 (denove kuba kahelaro, do sen novaj formoj)
(denove kuba kahelaro, do sen novaj formoj)
Aldone estas unu speciala plilongigita formo de la triangula (ebena) kahelaro kaj farita surbaze de ĝi plilongigita triangula prisma kahelaro (1 nova formo).
Aldone estas 5 specialaj kahelaroj kiu ne havas puran reflektan simetrion kaj estas konstruitaj de reflekte simetriaj formoj per operacioj plilongigo kaj turnigo.
R4, [4,3,4] grupo (kuba)
[redakti | redakti fonton]La regula kuba kahelaro, prezentis per simbolo de Schläfli {4,3,4}, donas 7 unikajn derivitajn unuformaj kahelaroj per tranĉaj operacioj. La edrotranĉita kuba kahelaro, estas inkluzivita por pleneco sed estas identa al la kuba kahelaro.
Relativaj kvantoj de ĉeloj laŭ pozicioj en kuba kahelaro estas 1, 4, 4, 1 por pozicioj (0), (1), (2), (3) respektive. Tamen, ĉiu vertico povas esti najbara al diversa kvanto de ĉeloj de en diversaj pozicioj.
| Kahelaro | Indeksoj | Figuro de Coxeter-Dynkin Simbolo de Schläfli |
Kvantoj de ĉeloj ĉirkaŭ ĉiu vertico laŭ pozicioj en kuba kahelaro | Solidoj (parta) | Perspektiva vida | Vertica figuro | |||
|---|---|---|---|---|---|---|---|---|---|
| (0) | (1) | (2) | (3) | ||||||
| Kuba kahelaro | J11,15 A1 W1 G22 |
t0{4,3,4} |
8 kuboj (4.4.4) |

|

|
 Okedro | |||
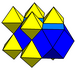
| Rektigita kuba kahelaro | J12,32 A15 W14 G7 |
t1{4,3,4} |
2 okedroj (3.3.3.3) |
4 kubokedroj (3.4.3.4) |
|

|
 Paralelepipedo | ||
| Senpintigita kuba kahelaro | J13 A14 W15 G8 |
t0,1{4,3,4} |
1 okedro (3.3.3.3) |
4 senpintigitaj kuboj (3.8.8) |

|

|
 Kvadrata piramido | ||
| Laterotranĉita kuba kahelaro | J14 A17 W12 G9 |
t0,2{4,3,4} |
1 kubokedro (3.4.3.4) |
2 kuboj (4.4.4) |
2 malgrandaj rombokub-okedroj (3.4.4.4) |

|

|
 Kojno | |
| Edrotranĉita kuba kahelaro (la sama kiel regula kuba kahelaro) |
J11,15 | t0,3{4,3,4} |
1 kubo (4.4.4) |
3 kuboj (4.4.4) |
3 kuboj (4.4.4) |
1 kubo (4.4.4) |

|

|
 okedro |
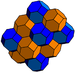
| Dutranĉita kuba kahelaro | J16 A3 W2 G28 |
t1,2{4,3,4} |
2 senpintigitaj okedroj (4.6.6) |
2 senpintigitaj okedroj (4.6.6) |
|

|
 Izocela kvaredro | ||
| Rektigitotranĉita kuba kahelaro | J17 A18 W13 G25 |
t0,1,2{4,3,4} |
1 senpintigita okedro (4.6.6) |
1 kubo (4.4.4) |
2 grandaj rombokub-okedroj (4.6.8) |

|
 Neregula kvaredro | ||
| Edroverticotranĉita kuba kahelaro | J18 A19 W19 G20 |
t0,1,3{4,3,4} |
1 malgranda rombokub-okedro (3.4.4.4) |
1 kubo (4.4.4) |
2 oklateraj prismoj (4.4.8) |
1 senpintigita kubo (3.8.8) |

|

|
 Oblikva trapeza piramido |
| Entutotranĉita kuba kahelaro | J19 A22 W18 G27 |
t0,1,2,3{4,3,4} |
1 granda rombokub-okedro (4.6.8) |
1 oklatera prismo (4.4.8) |
1 oklatera prismo (4.4.8) |
1 granda rombokub-okedro (4.6.8) |

|

|
 Malregula kvaredro |
| Kvaredro-okedra kahelaro (alternita kuba kahelaro) |
J21,31,51 A2 W9 G1 |
h0{4,3,4} |
6 okedroj (3.3.3.3) |
8 kvaredroj (3.3.3) |

|

|
 Kubokedro | ||
S4, h[4,3,4] grupo
[redakti | redakti fonton]La S4 grupo donas 11 derivajn formoj per tranĉaj operacioj, el ili 4 estas novaj unuformaj kahelaroj.
Verticoj estas indeksataj kiel 0,1,0',3 kaj 0' estas interŝanĝebla 0.
| Kahelaro | Indeksoj | Figuro de Coxeter-Dynkin | Kvantoj de ĉeloj ĉirkaŭ ĉiu vertico laŭ pozicioj en alternita kuba kahelaro | Solidoj (parta) | Perspektiva vida | Vertica figuro | |||
|---|---|---|---|---|---|---|---|---|---|
| (0) | (1) | (0') | (3) | ||||||
| Kvaredro-okedra kahelaro (alternita kuba kahelaro) | J21,31,51 A2 W9 G1 |
6 okedroj (3.3.3.3) |
8 kvaredroj (3.3.3) |

|

|
 Kubokedro | |||
| Senpintigita alternita kuba kahelaro | J22,34 A21 W17 G10 |
1 kubokedro (3.4.3.4) |
2 senpintigitaj okedroj (4.6.6) |
2 senpintigitaj kvaredroj (3.6.6) |

|

|

| ||
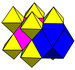
| Rektigita kuba kahelaro (rektigita alternita kuba kahelaro) |
J12,32 A15 W14 G7 |
2 kubokedroj (3.4.3.4) |
2 kubokedroj (3.4.3.4) |
2 okedroj (3.3.3.3) |
|

|
 Paralelepipedo | ||
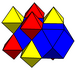
| Rektigita kuba kahelaro (laterotranĉita alternita kuba kahelaro ???) |
J12,32 A15 W14 G7 |
1 okedro (3.3.3.3) |
1 okedro (3.3.3.3) |
4 kubokedroj (3.4.3.4) |
|

|
 Paralelepipedo | ||
| Dutranĉita kuba kahelaro (rektigitotranĉita alternita kuba kahelaro ???) |
J16 A3 W2 G28 |
1 senpintigita okedro (4.6.6) |
1 senpintigita okedro (4.6.6) |
2 senpintigitaj okedroj (4.6.6) |

|

|
 Izocela kvaredro | ||
| Senpintigita kuba kahelaro (dulaterotranĉita alternita kuba kahelaro ???) |
J13 A14 W15 G8 |
2 senpintigitaj kuboj (3.8.8) |
2 senpintigitaj kuboj (3.8.8) |
1 okedro (3.3.3.3) |

|

|
 Kvadrata piramido | ||
| Kuba kahelaro (trirektigita alternita kuba kahelaro ???) |
J11,15 A1 W1 G22 |
4 kuboj (4.4.4) |
4 kuboj (4.4.4) |

|

|
 Okedro | |||
| Alterne edrotranĉita kuba kahelaro | J23 A16 W11 G5 |
1 kubo (4.4.4) |
3 malgrandaj rombokub-okedroj (3.4.4.4) |
1 kvaredro (3.3.3) |

|

|

| ||
| Laterotranĉita kuba kahelaro (edrolaterotranĉita alternita kuba kahelaro ???) |
J14 A17 W12 G9 |
1 malgranda rombokub-okedro (3.4.4.4) |
2 kuboj (4.4.4) |
1 malgranda rombokub-okedro (3.4.4.4) |
1 kubokedro (3.4.3.4) |

|

|
 Kojno | |
| Alterne edroverticotranĉita kuba kahelaro | J24 A20 W16 G21 |
1 senpintigita kubo (3.8.8) |
2 grandaj rombokub-okedroj (4.6.8) |
1 senpintigita kvaredro (3.6.6) |

|

|

| ||
| Rektigitotranĉita kuba kahelaro (entutotranĉita alternita kuba kahelaro ???) |
J17 A18 W13 G25 |
1 granda rombokub-okedro (4.6.8) |
1 kubo (4.4.4) |
1 granda rombokub-okedro (4.6.8) |
1 senpintigita okedro (4.6.6) |

|
 Malregula kvaredro | ||
P4 grupo
[redakti | redakti fonton]Estas 5 formoj de la grupo P4, nur la kvarona kuba kahelaro estas nova.
| Kahelaro | Indeksoj | Figuro de Coxeter-Dynkin Simbolo de Schläfli |
Kvantoj de ĉeloj ĉirkaŭ ĉiu vertico laŭ pozicioj | Solidoj (parta) | Perspektiva vida | Vertica figuro | |||
|---|---|---|---|---|---|---|---|---|---|
| (0) | (1) | (2) | (3) | ||||||
| Kvaredro-okedra kahelaro (alternita kuba kahelaro) |
J21,31,51 A2 W9 G1 |
h0{4,3,4} |
4 kvaredroj (3.3.3) |
6 okedroj (3.3.3.3) |
4 kvaredroj (3.3.3) |

|

|
 Kubokedro | |
| Rektigita kuba kahelaro | J12,32 A15 W14 G7 |
2 kubokedroj (3.4.3.4) |
1 okedroj (3.3.3.3) |
2 kubokedroj (3.4.3.4) |
1 okedroj (3.3.3.3) |

|

|
 Paralelepipedo | |
| Kvarona kuba kahelaro | J25,33 A13 W10 G6 |
1 kvaredro (3.3.3) |
1 kvaredro (3.3.3) |
3 senpintigitaj kvaredroj (3.6.6) |
3 senpintigitaj kvaredroj (3.6.6) |

|

|

| |
| Senpintigita alternita kuba kahelaro | J22,34 A21 W17 G10 |
1 senpintigita kvaredro (3.6.6) |
1 kubokedro (3.4.3.4) |
1 senpintigita kvaredro (3.6.6) |
2 senpintigitaj okedroj (4.6.6) |

|

|

| |
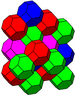
| Dutranĉita kuba kahelaro | J16 A3 W2 G28 |
1 senpintigita okedro (4.6.6) |
1 senpintigita okedro (4.6.6) |
1 senpintigita okedro (4.6.6) |
1 senpintigita okedro (4.6.6) |
|

|
 Izocela kvaredro | |
Prismaj kolonoj
[redakti | redakti fonton]11 prismaj kahelaroj estas konstruataj per kolonigo de la 11 unuformaj ebenaj kahelaroj, kreante paralelajn tavolojn de prismoj. Unu el ĉi tiuj kahelaroj estas la kuba kahelaro, listigita pli supre. La vertica figuro de ĉiuj la 10 novaj kahelaroj estas malregula dupiramido kies edroj estas izocelaj trianguloj.
Notu, ke nomo de ĉi tia kahelaro "prismigita riproĉa seslatera kahelaro" estas pli bona ol iam uzata nomo "riproĉa seslatera prisma kahelaro", ĉar komence de seslatera kahelaro unue ĝi estas riproĉigita kaj nur poste el ĝi estas farataj prismoj. Sed la dua nomo signifas ke seslateraj prismoj estas riproĉigitaj, kio ne estas la vero.
La R3xW2, [4,4] x [∞], prisma grupo
[redakti | redakti fonton]Estas nur 3 unikaj kahelaroj de la kvadrata kahelaro, sed ĉiuj 6 kahelaraj tranĉoj estas listitaj ĉi tie por pleneco, kaj kahelaraj bildoj estas montrita kun koloroj respektivaj al ĉiu formo.
| Kahelaro | Indeksoj | Figuro de Coxeter-Dynkin Simbolo de Schläfli |
Fonta ebena kahelaro | Bildo de fonta ebena kahelaro | Solidoj (parta) |
|---|---|---|---|---|---|
| Kuba kahelaro (kvadrata prisma kahelaro) |
J11,15 A1 G22 |
{4,4} x {∞} |
Kvadrata kahelaro (4.4.4.4) | 
|

|
| Prismigita senpintigita kvadrata kahelaro (dutranĉita kvadrata prisma kahelaro) |
J45 A6 G24 |
t0,1{4,4} x {∞} |
Senpintigita kvadrata kahelaro (4.8.8) | 
|

|
| Kuba kahelaro (Rektigita kvadrata prisma kahelaro) |
J11,15 A1 G22 |
t1{4,4} x {∞} |
Kvadrata kahelaro (4.4.4.4) (rektigita kvadrata kahelaro) |

|

|
| Kuba kahelaro (laterotranĉita kvadrata prisma kahelaro) |
J11,15 A1 G22 |
t0,2{4,4} x {∞} |
Kvadrata kahelaro (4.4.4.4) (laterotranĉita kvadrata kahelaro) |

|

|
| Prismigita senpintigita kvadrata kahelaro (prismigita entutotranĉita kvadrata kahelaro) |
J45 A6 G24 |
t0,1,2{4,4} x {∞} |
Senpintigita kvadrata kahelaro (4.8.8) (entutotranĉita kvadrata kahelaro) |

|

|
| Prismigita riproĉa kvadrata kahelaro | J44 A11 G14 |
s{4,4} x {∞} |
Riproĉa kvadrata kahelaro (3.3.4.3.4) | 
|

|
La V3xW2, [6,3] x [∞] prisma grupo
[redakti | redakti fonton]Plilongigita formo de la triangula (ebena) kahelaro
[redakti | redakti fonton]| Kahelaro | Indeksoj | Figuro de Coxeter-Dynkin Simbolo de Schläfli |
Fonta ebena kahelaro | Bildo de fonta ebena kahelaro | Solidoj (parta) |
|---|---|---|---|---|---|
| Plilongigita triangula prisma kahelaro | J65 A11' G13 |
{3,6}:e x {∞} | Plilongigita triangula kahelaro (3.3.3.4.4) | 
|

|
Turnitaj kaj plilongigitaj formoj
[redakti | redakti fonton]Ĉiu el tri novaj unuformaj kahelaroj estas generitaj per disigo de iu el la pli supre listigitaj kahelaroj tie kie ĝiaj edroj formas kontinuan ebenon, kaj turno de alternaj tavoloj je 60 aŭ 90 gradoj (turno) aŭ enigo de tavolo de prismoj (plilongigo).
La plilongigita alternita kuba kahelaro kaj turnoplilongigita alternita kuba kahelaro havas la saman vertican figuron, sed ne estas egalaj. En la plilongigita formo, ĉiu prismo tuŝas kvaredron je unu triangula bazo kaj okedron je la alia. En la turnoplilongigita formo, prismoj kiuj tuŝas kvaredrojn je ambaŭ bazoj alternas kun prismoj kiuj tuŝas okedrojn je ambaŭ bazoj.
La turnoplilongigita triangula prisma kahelaro havas la sama vertican figuron kiel unu el la ebenaj prismaj kahelaroj; la du povas esti derivitaj de la turnita triangula prisma kahelaro kaj ebena triangula prisma kahelaro respektive, per enigo de tavoloj de kuboj.
| Kahelaro | Indeksoj | Simbolo | Kvantoj de ĉeloj ĉirkaŭ ĉiu vertico | Solidoj (parta) | Perspektiva vida | Vertica figuro |
|---|---|---|---|---|---|---|
| Turnita alternita kuba kahelaro | J52 A2' G2 |
h{4,3,4}:g | kvaredro (8) okedro (6) |

|

|

|
| Turnoplilongigita alternita kuba kahelaro | J61 A? G3 |
h{4,3,4}:ge | triangula prismo (6) kvaredro (4) okedro (3) |

|

|

|
| Plilongigita alternita kuba kahelaro | J62 A? G4 |
h{4,3,4}:e | triangula prismo (6) kvaredro (4) okedro (3) |

|

|

|
| Turnita triangula prisma kahelaro | J63 A? G12 |
{3,6}:g x {∞} | triangula prismo (12) | 
|

|

|
| Turnoplilongigita triangula prisma kahelaro | J64 A? G15 |
{3,6}:ge x {∞} | triangula prismo (6) kubo (4) |

|

|

|
Uzoj
[redakti | redakti fonton]Ĉiuj 28 el ĉi tiuj kahelaroj estas trovitaj en kristalaj ordigoj.
La kvaredra-okedra kahelaro (alternita kuba kahelaro) estas speciale grava pro tio ke ĝiaj verticoj formas kuban proksiman pakon de sferoj.
Vidu ankaŭ
[redakti | redakti fonton]- Listo de unuformaj ebenaj kahelaroj
- Listo de regulaj hiperpluredroj - ankaŭ pri regulaj kahelaroj
- Regula pluredro
- Regula plurĉelo
- Duonregula plurĉelo - ankaŭ pri duonregulaj 3-kahelaroj
- Unuforma pluredro
- Unuforma plurĉelo
Eksteraj ligiloj
[redakti | redakti fonton]- Eric W. Weisstein, Kahelaro en MathWorld.
- VRML modeloj de unuformaj kahelaroj en 3-spaco
- Rudimentaj kahelaroj Arkivigite je 2007-10-12 per la retarkivo Wayback Machine
- Unuformaj dispartigoj de 3-spaco, iliaj relativaj kaj enigo PDF, 1999
- La unuformaj pluredroj
- Virtualaj realaj pluredroj La enciklopedio de pluredroj
















