Eŭklido
| Eŭklido greke Εὐκλείδης | ||
|---|---|---|
 Moderna imagita portreto
| ||
| Persona informo | ||
| Εὐκλείδης | ||
| Naskonomo | Εὐκλείδης | |
| Naskiĝo | 325 a. K. en Aleksandrio, Egiptio | |
| Morto | 265 a. K. en Aleksandrio, Egiptio | |
| Lingvoj | antikva greka vd | |
| Loĝloko | Aleksandrio vd | |
| Ŝtataneco | Antikva Ateno vd | |
| Profesio | ||
| Okupo | matematikisto • verkisto vd | |
| Laborkampo | geometrio vd | |
| Verkado | ||
| Verkoj | Elementoj de Eŭklido ❦ sinteza geometrio vd | |
| vd | Fonto: Vikidatumoj | |
Eŭklido (greke Εὐκλείδης Eu̍kleídês; naskiĝis ĉirkaŭ 325 a. K.; mortis en 265 a.K.) estis greka geometro, kiu kompilis la Elementojn, faman verkon pri geometrio. La teksto enhavas tiamajn sciojn pri geometrio kaj estis uzata dum jarcentoj en okcidenta Eŭropo kiel lernolibro. La teksto komenciĝas per difinoj, postulatoj kaj ĝeneralaj opinioj pri la proceduroj kiel ricevi rezultojn per rigoraj geometriaj pruvoj. Eŭklido pruvis ankaŭ la tiel nomatan Duan teoremon de Eŭklido: "La nombro de primoj estas senfina". Li provis uzi algoritmon por trovi plej grandan komunan divizoron kaj por pruvi la teoremon de Pitagoro.
Vivo[redakti | redakti fonton]

Pri la vivo de la greka matematikisto Eŭklido nur malmulte konatas. Nek la jaro de lia naskiĝo, nek la loko estas ĝis nun establitaj. Li estis samtempulo de Arkimedo (287 a. K. - 212 a. K.). Iuj supozas, ke li naskiĝis ĉirkaŭ la jaro 360 a. K., verŝajne en Ateno, kaj tie edukiĝis ĉe la akademio de Platono. Aliaj indikas -325 kiel naskiĝjaro[1], sed laŭ la matematikisto Christian Velpryses, liaj vivodatoj estas tute nekonataj.[2]
Fakte la ŝlosilaj referencoj pri Eŭklido estis skribitaj jarcentoj post lia morto, fare de Proklo kaj Papo de Aleksandrio.[3] Proklo menciis Eŭklidon nur mallonge en sia Komentario pri la elementoj verkita en la 5-a jarcento, kie li skribis, ke Eŭklido estis la aŭtoro de la Elementoj, ke menciis lin Arkimedo kaj kiam Ptolemeo la 1-a demandis Eŭklidon, ĉu ne ekzistis vojo al geometrio pli mallonga ol tiu de la Elementoj, li respondis, ke "ne ekzistas reĝa vojo al geometrio". Kvankam la citaĵo de Eŭklido fare de Arkimedo estis taksita interpolado de postaj eldonistoj de liaj verkoj, oni daŭre supozas, ke Eŭklido verkis siajn tekstojn antaŭ tiuj de Arkimedo.[4][5] Krome la anekdoto pri la "reĝa vojo" estas pridubinda, ĉar ĝi similas rakonton pri Meneĥmo kaj Aleksandro la Granda.[6]
En la ununura alia ŝlosilreferenco al Eŭklido, Pappus mallonge menciis en la 4-a jarcento, ke Apolonio "pasigis tre longan tempon kun la lernantoj de Eŭklido en Aleksandrio, kaj tiel li akiris tian sciencan vestaĵon de pensado."[7]
Li tre verŝajne vivis en Aleksandrio dum la regado de Ptolemeo la 1-a (eble ankaŭ dum tiu de Ptolemeo la 2-a) kaj instruis tie matematikon.
Eŭklido famiĝis pro 13 lernolibroj, en kiuj li kompilis la tiamajn sciojn pri matematiko. La elementoj, kiel oni nomas tiujn librojn, estas la plej sukcesaj matematiklibroj de ĉiuj epokoj. Tiel tradukoj de tiuj libroj estis uzataj en Britujo ankoraŭ en la 19-a jarcento kiel oficialaj lernejaj libroj pri geometrio.
Ankaŭ la cirkonstancoj kaj dato de lia morto estas nekonataj.
La Elementoj[redakti | redakti fonton]

La Elementoj estas kompilo de geometriaj scioj kaj restis kerno de matematika instruado dum preskaŭ 2000 jaroj. Eblus ke neniu el la elementoj estus de Eŭklido mem, sed iliaj organizado kaj prezentado, kaj tiel verŝajne ankaŭ transdono, estas lia verko.
La Elementoj estas dividitaj en dek tri libroj. La libroj 1 ĝis 6 temas pri ebena geometrio, la libroj 7 ĝis 9 pri pitagora aritmetiko, la libro 10 pri la teorio de neracionalaj nombroj de Eŭdokso, kaj la libroj 11 ĝis 13 pri spaca geometrio. Finiĝas la libro per esploro de la ecoj de kvin regulaj pluredroj kaj klarigo de ilia ekzisto. La Elementoj estas rimarkindaj pro la klareco de prezentado kaj klarigo de la teoremoj. La Elementoj entenas la komencojn de la nombroteorio (jam konata de Archytas) kaj la konceptojn pri divideblo kaj pri la plej granda komuna divizoro, kalkulebla per la Eŭklida algoritmo. Eŭklido pruvis, ke ekzistas senfina nombro de primoj. En la libro 5 troviĝas la scioj pri proporcio de Eŭdokso, ĝeneraligo de aritmetiko al pozitivaj neracionalaj nombroj.
Pli ol miloj da eldonejoj manuskriptaj de la Elementoj estis publikigataj antaŭ la unua presita versio en 1482. La rigoro ne estas ĉiam tia de nuntempaj normoj, sed la metodo konsistis el deiro de aksiomoj, postulatoj kaj difinoj, por dedukti maksimumon de ecoj de la objektoj traktataj, ĉio ĉi en organizita tutaĵo, tute nova por la tiama epoko. La sukceso de la Elementoj devenas de iliaj organizado, sistemigo kaj matematika logiko. La plej lastaj esploroj pri historio de matematiko pruvas, ke Eŭklido ne estas la ununura aŭtoro de la Elementoj. Verŝajne ĉirkaŭis lin kolegaro de disĉiploj, kiuj ĉiuj partoprenis la ellaboron.
La geometrio tia, kia ĝi estis difinita de Eŭklido estis konsiderata dum jarcentoj kiel la geometrio, kaj malfacilis superi ĝin. Nikolaj Ivanoviĉ Lobaĉevskij estis la unua, kiu oficiale provis tion en 1826, sekvita de János Bolyai, sed la legendo diras, ke oni ne serioze traktis lin antaŭ la morto de Carl Friedrich Gauss, kiam oni malkovris inter ties malnetoj, ke ankaŭ li imagis neeŭklidajn geometriojn.
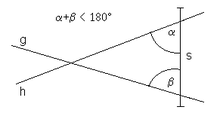
En siaj libroj Eŭlido uzas, por montri la ecojn de rektoj, la postulaton de Eŭklido, kiun oni esprimas nuntempe, dirante, ke tra punkto ekster rekto, pasas unu kaj nur unu paralelo al tiu rekto. La fama kvina postulato de la ebena eŭklida geometrio, nomata ankaŭ paralela aksiomo postulas, ke se rekta segmento s tranĉante du rektojn g kaj h formante du angulojn ene de la sama flanko de s α kaj β kune malpli grandaj ol du ortaj anguloj, tiam la du rektoj g kaj h renkontiĝas ĉe tiu flanko de s, kie situas la anguloj α kaj β. Se do du rektoj tranĉas rektan segmenton (aŭ rekton), tiel ke la du anguloj malfermitaj unuflanke de la rekta segmento kaj aliflanke de la du rektoj estas malpli grandaj ol 180°, tiam la du rektoj renkontiĝas tiuflanke kaj kune kun la rekta segmento (aŭ la tria rekto) limigas triangulon.
Ekzistas esence tri specoj de geometrio:
- tiu, kiu akceptas la postulaton de Eŭklido, nomata ebena geometrio aŭ eŭklida geometrio,
- tiu, kiu akceptas la postulaton, ke tra punkto ekster rekto, pasas neniu paralelo al tiu rekto, nomata sfera geometrio aŭ riemanna geometrio,
- tiu, kiu akceptas la postulaton, ke tra punkto ekster rekto, pasas senfina nombro de paraleloj al tiu rekto, nomata geometrio de Lobaĉevskij.
Riemann montris, ke modelo de sfera geometrio estas sfero kaj la rektoj korespondas al meridianoj aŭ grandaj cirkloj. Poincaré donis modelon de la geometrion de Lobaĉevskij. Ĉar ekzistas modeloj por la tri geometrioj ne ekzistas kialo privilegii unu pli ol la aliaj. La teorio de relativeco de Einstein fine montris la kurbiĝon de la spaco, kaj kiam la spaco kurbiĝas, ĝi forlasas sian aspekton eŭklidan.
Muzikteorio[redakti | redakti fonton]
En la muzikteoria verko de Eŭklido Divido de kanono (greke Katatomē kanonos, latine Sectio canonis), kiu estas konsiderata aŭtenta, temas pri la muzikteorio de Arĥitas kaj starigis ĝin sur pli solidan akustikan bazon, tio estas sur frekvencojn de vibroj (li parolis pri ofteco de movoj).
Li ĝeneraligis la frazon de Arĥitas pri la neracionaleco de la kvadrata radiko kaj pruvis ĝenerale la neracionalecon de iuj radikoj . La kialo de tiu genia ĝeneraligo estas lia kontraŭtezo kontraŭ la harmoniko de Aristokseno, kiu konstruiĝas je raciaj obligoj de la tono (duontono ... tonono). Ĉar en la pitagora harmoniko la tono (plentono)la proporcion 9:8, kio instigis al Eŭklido lian kontraŭtezon "La tono divideblas nek en du ne en plurajn samajn erojn"; ĝin kondiĉas tamen kunmezureblaj frekvencoj, kiujn oni supozis en la pitagoran harmonikon ĝis la fino de la 16-a jarcento (Simon Stevin). La kontraŭtezon "La oktavo estas pli malgranda ol 6 plentonoj" li baziĝis je la kalkulo de la pitagora komao. Krome la Divido de kanono de Eŭklido entenas - kiel indikas la titolo - la plej malnova dokumentita reprezento de tonsistemo ĉe kanono, dividita kordo, tio estas pitagora reinterpreto de la kompleta diatona tonsistemo de Aristokseno, kio vastigis la harmonion de Filolao.
La tonsistemo de Eŭklido iĝis la bazo de la moderna tonsistemo kun la nuntempe kutima nomado per tonliteroj de Odo de Cluny.
Citaĵoj[redakti | redakti fonton]

|
|
Verko[redakti | redakti fonton]
- Elementoj. Libroj 1-13.
- germane Clemens Thaer (4-a eldono, Harri Deutsch, Frankfurt a.M. 2003. ISBN 3-8171-3413-4), en franca
- france Denis Henrion, Les quinze livres des éléments géométriques d'Euclide (1632) ĉe Gallica. La du lastaj libroj estas apokrifaj, la 14-a estus de Hypsicles).
- Data.
- germane Laŭ teksto de Menge tradukita el la greka al germana kaj eldonita de Clemens Thaer. Springer, Berlin 1962
- Divido de kanono
- germane Teilung des Kanons (sectio canonis), eld. de H. Menge en: Euclidis opera omnia, vol. 8, Leipzig 1916, 158-183
- Sectio canonis
- germane Noveldonita, tradukita kaj komentita en: Busch, Oliver: Logos syntheseos : die euklidische Sectio canonis, Aristoxenos, und die Rolle der Mathematik in der antiken Musiktheorie, Hildesheim, 2004, ISBN/ISSN: 3-487-11545-X
- Optika
- Pri la divido de figuroj (parte konservita en araba traduko.
- De aliaj verkoj konatas nur la titoloj kiel Pseudaria (Paralogismoj), Katoptrika kaj Phainomena (astronomio).
Bibliografio[redakti | redakti fonton]
- Scholia in Elementa, en Euclidis Elementa, eldonita de J. L. Heiberg, vol. 5 (Leipzig, 1888), p. 71-738.
- Marcel Boll, Euclide, Galilée, Newton, Einstein, Parizo, 1922.
- G. Kayas, Vingt-trois siècles de tradition euclidienne (Dudek tri jarcentoj de tradicio eŭklida), Palaiseau, 1977.
- Christian Velpry, Euclide l'Africain ou la Géométrie restituée, eld. Menaibuc, Parizo, p. 113, isbn 2-911372-55-7. Prezentita kiel "enketo matematika kaj historia" de franca profesoro pri matematiko, tiu verko kontraŭas la kutimajn teoriojn pri Eŭklido. Arkivigite je 2010-02-10 per la retarkivo Wayback Machine
- Wilfried Neumaier: Was ist ein Tonsystem? (Kio estas tonsistemo?), Frankfurt am Main, Bern, New York, 1986, ĉap. 6, Die „Teilung des Kanons“ des Eukleides (La "divido de kanono"" de Eŭklido).
- Christoph J. Scriba, Peter Schreiber: 5000 Jahre Geometrie. Geschichte, Kulturen, Menschen (5000 jaroj da geometrio. Historio, kulturoj, homoj), Springer, Berlin 2005, ISBN 3-540-22471-8 (p.49-65).
- Max Steck: Bibliographia Euclideana. Die Geisteslinien der Tradition in den Editionen der „Elemente“ des Euklid (um 365-300). Handschriften, Inkunabeln, Frühdrucke (16.Jahrhundert). Eldonejoj Opera minora (16-a ĝis 20-a jarcento). Represaĵo, eldonita de Menso Folkerts. Hildesheim: Gerstenberg, 1981.
- Bartel Leendert van der Waerden: Geometry and Algebra in Ancient Civilizations. (Geometrio kaj alĝebro en antikvaj civilizoj.) Springer, Berlin 1983, ISBN 3-540-12159-5.
Referencoj[redakti | redakti fonton]
- ↑ france Euclide d'Alexandrie, bibmath.net Arkivigite je 2006-05-03 per la retarkivo Wayback Machine
- ↑ Euclide l'Africain ou la Géométrie restituée, Christian Velpry, eld. Menaibuc, Parizo, p. 113, isbn 2-911372-55-7, interrete legeble [1] Arkivigite je 2010-02-10 per la retarkivo Wayback Machine
- ↑ Joyce, David. Euclid. Clark University Department of Mathematics and Computer Science. [2]
- ↑ Morrow, Glen. A Commentary on the first book of Euclid's Elements
- ↑ Euclid of Alexandria. The MacTutor History of Mathematics archive.
- ↑ Boyer, p. 1.
- ↑ Heath (1956), p. 2.
- ↑ Latine: "Quod erat demonstrandum."
Vidu ankaŭ[redakti | redakti fonton]
- Elementoj de Eŭklido
- Eŭklida algoritmo
- David Hilbert
- Neeŭklidaj geometrioj
- Unua teoremo de Eŭklido
- 4354 Eŭklido
Eksteraj ligiloj[redakti | redakti fonton]
- La elementoj: ĉiuj dek tri libroj en la lingvoj hispana, katalana, angla, germana, portugala, araba, itala, rusa kaj ĉina.
- La elementoj de Eŭklido (ĉiuj 13 libroj en la angla)
- La elementoj de Eŭklido (ĉiuj 13 libroj en la greka kun latina traduko) (PDF)
- Die sechs ersten Bücher Evclidis, Deß Hochgelaehrten weitberuembten, Griechischen Philosophi und Mathematici: von den anfaengen vnd fundamenten der Geometriae (germane). Amsterdamo 1618, interreta eldono de la saksa landa biblioteko - Staats- und Universitätsbibliothek Dresden
- Euclidis Megarensis ... sex libri priores, de Geometricis principiis. Basileae 1550, interreta eldono de la saksa landa biblioteko - Staats- und Universitätsbibliothek Dresden
- Euclidis Megarensis Mathematici Clarissimi Elementorum geometricorum Lib. XV. Basileae 1537, interreta eldono de la saksa landa biblioteko - Staats- und Universitätsbibliothek Dresden
- Elementale Geometricum. Argentorati 1529, interreta eldono de la saksa landa biblioteko - Staats- und Universitätsbibliothek Dresden
- Elementorum Libri XV. Coloniae 1627, interreta eldono de la saksa landa biblioteko - Staats- und Universitätsbibliothek Dresden
- Perseus Euklid Arkivigite je 2010-01-27 per la retarkivo Wayback Machine. Informoj de Perseus kun traduko kaj aliaj fontoj kaj ligiloj.
- Privata ttt-ejo pri Eŭklido kaj ties samtempuloj




![{\displaystyle {\sqrt[{n}]{\tfrac {m+1}{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca3864b8b0e7089d0adf4aa06c0952e392781d5d)