Funkcio (matematiko)

Reviziita versio de ĉi tiu paĝo, aprobita je 12 apr. 2015, estis bazita sur ĉi tiu versio.

Matematikaj funkcioj
fonta aro, cela aro • bildo, malbildo • bildaro, argumentaro
Fundamentaj funkcioj
Algebraj funkcioj: konstanta • lineara • kvadrata • polinoma • racionala • Transformo de Möbius Aliaj funkcioj: trigonometriaj • inversa trigonometria • hiperbola • eksponenta • logaritma • potenca
Specialaj funkcioj
erara • β • Γ • ζ • η • W de Lambert • de Bessel
Nombroteoriaj funkcioj:
τ • σ • de Möbius • φ • π • λ
Ecoj:
totaleco kaj parteco • pareco kaj malpareco • monotoneco • bariteco • periodeco • disĵeteco • surĵeteco • dissurĵeteco kontinueco • derivaĵeco • integralebleco

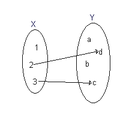
Se ni havas du arojn X kaj Y, oni povas establi diversajn konformecojn inter iliaj elementoj, kiujn oni esprimas per f, g, h, … simboloj. La konformeco inter aroj X kaj Y, estas nomata funkcio (aŭ bildigo), se al ĉiu elemento de X konformas unusola elemento el Y. La signo de la funkcio estas : y = f(x), kie x estas sendependa variablo, kaj y - dependa variablo.

Sendependa variablo (argumento) - la variablo, por ĉiu el kies valoroj estas donita responda valoro de funkcio.

Dependa variablo - la variablo donita per la valoroj de de funkcio; ekz. en la funkcio sin, x - estas la sendependa variablo (argumento), dum sin x estas dependa variablo.

Aro X nomiĝas kampo de difino aŭ argumentaro, simbole D(f), kaj aro Y - kampo de valoroj aŭ valoraro, simbole E(f). Funkcio povas esti donita, se estas konata ĝia argumentaro kaj regulo de konformeco. Dume, la rimedoj por esprimo de la regulo povas esti diversaj:

Tabela - per la vicoj de argumentoj kaj ĝiaj konformaj signifoj;
Grafika - la aro de la punktoj M(x;y) sur la kartezia sistemo, prezentita laŭ formo de la rekto aŭ kurbo;
Analiza - per formulo, ekz. y = 3 x² + 1.

Derivaj difinoj

Funkcio estas kreskanta sur iu aro, se por ajnaj elementoj de la aro x₁ < x₂, la malegalaĵo f(x₁) < f(x₂) estas vera. Se por x₁ < x₂, veras la alia malegalaĵo f(x₁) > f(x₂), la funkcio nomiĝas malkreskanta. Ekzemple, funkcio y=x² estas malkreskanta en la intervalo ]-∞;0] kaj estas kreskanta en la intervalo [0;+∞[.

Funkcio estas para, se la kampo de difino estas simetria rilate al 0 kaj por ajna x ∈ D(f) estas vera egelaĵo : f(-x) =f(x). Kaj ĝi nomiĝas malpara, se veras : f(-x) = -f(x). Ekzemple, y=x² funkcio estas para, kaj y=x aŭ y=x³ estas malparaj.

Funkcio estas perioda kun periodo p, kiu ne egalas al 0, se por ajna x ∈ D(f) la nombroj x-p kaj x+p ankaŭ apartenas al D(f) kaj veras la egalaĵo: f(x+p) = f(x), ankaŭ f(x) = f(x-p) kaj f(x) = f(x+kp), kie k estas entjero.