Malbildo
| Matematikaj funkcioj |
|---|
| fonta aro, cela aro • bildo, malbildo • bildaro, argumentaro |
| Fundamentaj funkcioj |
| Algebraj funkcioj: konstanta • lineara • kvadrata • polinoma • racionala • Transformo de Möbius Aliaj funkcioj: trigonometriaj • inversa trigonometria • hiperbola • eksponenta • logaritma • potenca |
| Specialaj funkcioj |
| erara • β • Γ • ζ • η • W de Lambert • de Bessel |
| Nombroteoriaj funkcioj: |
| τ • σ • de Möbius • φ • π • λ |
| Ecoj: |
| totaleco kaj parteco • pareco kaj malpareco • monotoneco • bariteco • periodeco • disĵeteco • surĵeteco • dissurĵeteco kontinueco • derivaĵeco • integralebleco |
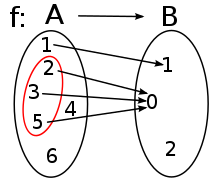
En matematiko, la malbildo[1] aŭ prabildo aŭ kontraŭbildo de elemento en cela aro de funkcio estas la aro de tiuj elementoj de la fonta aro de la funkcio, kies bildo estas la koncerna elemento. Pli ĝenerale, oni povas analoge difini la malbildon de subaro de la cela aro. Tiusence, la argumentaro de funkcio estas la malbildo de ĝia cela aro.
Difino[redakti | redakti fonton]
Konsideru bildigon
- ,
kies fonta aro estas kaj kies cela aro estas . Se estas subaro de la cela aro , la malbildo de per estas la subaro de la fonta aro difinita jene:
- .
Se estas elemento de la cela aro, la malbildo de per [2]:Difino 2.2.1 estas la malbildo de la unuopo :
- .
Ecoj[redakti | redakti fonton]
La malbildo de la cela aro de funkcio estas ties argumentaro; ankaŭ la malbildo de la bildaro de la funkcio estas ties argumentaro.
La malbildo de unuopo ne nepre estas unuopo — ĝi povas enhavi neniun aŭ plurajn elementojn.
La malbildo de la malplena aro estas la komplemento de la argumentaro de la funkcio en ties cela aro.
Ekzemplo[redakti | redakti fonton]
Por la funkcio
- ,
la malbildo de 4 estas {−½, ½}, kaj la malbildo de la malplena aro estas {0}.
Vidu ankaŭ[redakti | redakti fonton]
Referencoj[redakti | redakti fonton]
- ↑ Nova Plena Ilustrita Vortaro de Esperanto: mal/bild/o
- ↑ Matthias, Ulrich. (1995-10) Fundamentoj de lineara algebro (esperante). Neckarhausen: Eldonita de la aŭtoro.
















![{\displaystyle f^{-1}[M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/926fa7c725292b1fd0156997eb7197b0b5253eca)
![{\displaystyle f^{-1}[M]=\{\,x\in A\,|\,f(x)\in M\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22ce9a9589a48e0469ce7ee13fc967bb6dc3ecce)



![{\displaystyle f^{-1}(b):=f^{-1}[\{b\}]=\{x\in A\mid f(x)=b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d544695bdbacb93bcfd7193b1206dc2c4db107a5)

