Divizora funkcio
| Matematikaj funkcioj |
|---|
| fonta aro, cela aro • bildo, malbildo • bildaro, argumentaro |
| Fundamentaj funkcioj |
| Algebraj funkcioj: konstanta • lineara • kvadrata • polinoma • racionala • Transformo de Möbius Aliaj funkcioj: trigonometriaj • inversa trigonometria • hiperbola • eksponenta • logaritma • potenca |
| Specialaj funkcioj |
| erara • β • Γ • ζ • η • W de Lambert • de Bessel |
| Nombroteoriaj funkcioj: |
| τ • σ • de Möbius • φ • π • λ |
| Ecoj: |
| totaleco kaj parteco • pareco kaj malpareco • monotoneco • bariteco • periodeco • disĵeteco • surĵeteco • dissurĵeteco kontinueco • derivaĵeco • integralebleco |


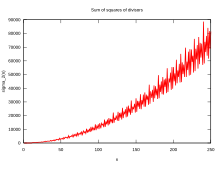
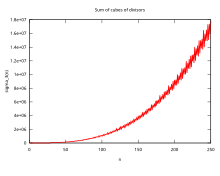
En nombroteorio, la divizora funkcio estas aritmetika funkcio rilata al divizoroj de entjero.
Difino[redakti | redakti fonton]
La funkcio, kiu prezentas sumon de pozitivaj divizoroj σx(n) estas difinita kiel la sumo de la x-aj potencoj de ĉiuj pozitivaj divizoroj de n, aŭ
La notacia stilo d(n) kaj τ(n) (la funkcio τ) estas uzata ankaŭ por σ0(n), t.e. la kvanto de divizoroj de n. Se x estas 1, la funkcio estas identa al la funkcio σ, kaj la suba indico estas ofte neskribata, do σ(n) estas ekvivalenta al σ1(n).
La obla suma funkcio estas sumo de la propraj divizoroj (tio estas, la divizoroj malinkluzivante n mem), estas s(n)=σ1(n)-n; la obla vico de n estas formita per multfoja aplika de la obla suma funkcio.
Ekzemplo[redakti | redakti fonton]
Ekzemple, σ0(12) estas la kvanto de la divizoroj de 12:
- σ0(12)=10+20+30+40+60+120=1+1+1+1+1+1=6
kaj σ1(12) estas la sumo de ĉiuj divizoroj:
- σ1(12)=11+21+31+41+61+121=1+2+3+4+6+12=28
Ecoj[redakti | redakti fonton]
Por primo p:
- d(p)=2
- d(pn)=n+1
- σ(p)=p+1
Por ĉiu n>2:
- 1<d(n)<n
- σ(n)>n
La divizora funkcio estas multiplika funkcio, sed ne plene multiplika funkcio. La konsekvenco de ĉi tio estas tiu ke, se
kie estas la kvanto de diversaj primaj faktoroj de n, pi estas la i-a prima faktoro, kaj ai estas la maksimuma povo de pi per kiu n estas dividebla, do
kiu estas ekvivalento al la utila formulo:
Ekvacio por kalkulo de d(n) estas
Ekzemple, se n estas 24, estas du primaj faktoroj (p1 estas 2; p2 estas 3); 24 estas produto de 23×31, a1 estas 3 kaj a2 estas 1. Do d(24) estas:
(la ok divizoroj estas 1, 2, 4, 8, 3, 6, 12, kaj 24).
Funkcio de sumo de la propraj divizoroj s(n) estas la uzata por difini perfektajn nombrojn, por kiu s(n)=n. Se s(n)>n do n estas abunda nombro kaj se s(n)<n do n estas manka nombro.
En 1984, Roger Heath-Brown pruvis ke
- d(n)=d(n+1)
okazas malfinie ofte.
Seria elvolvaĵo[redakti | redakti fonton]
La divizora funkcio povas esti skribita kiel finia trigonometria serio
sen eksplicita referenco al la divizoroj de n.
Seriaj rilatoj[redakti | redakti fonton]
Du serioj de Dirichlet engaĝantaj la divizoran funkcion estas:
kaj
Serio de Lambert engaĝanta la divizoran funkcion estas:
por ajna kompleksa nombro |q|≤1 kaj a. Ĉi tiu sumado ankaŭ aspektas kiel la serio de Fourier de la serio de Eisenstein kaj la invariantoj de la elipsa funkcio de Weierstrass.
Asimptota kreskado[redakti | redakti fonton]
En malgranda o skribmaniero, la divizora funkcio plenumas la jenan neegalaĵon:
En granda O skribmaniero, Dirichlet montris ke la averaĝa ordo de la divizora funkcio kontentigas jenan neegalaĵon
kie estas konstanto de Eŭlero-Mascheroni. Plibonigo de la baro en ĉi tiu formulo estas konata kiel la divizora problemo de Dirichlet
La konduto de la σ funkcio estas malregula. La kreska kurzo de la σ funkcio povas esti esprimita kiel:
kie limsup estas la limigo supera. Ĉi tiu rezulto estas teoremo de Thomas Hakon Grönwall, publikigita en 1913.
En 1984 Guy Robin pruvis ke
- por n>5040
estas vera se kaj nur se la rimana hipotezo estas vera. La plej granda sciata valoro kiu malverigas la neegalaĵon estas n=5040. Se la rimana hipotezo estas vera, ne estas pli grandaj esceptoj. Se la hipotezo estas malvera tiam estas malfinia kvanto da valoroj n tiaj por kiu la neegalaĵo estas malvera.
Rilatanta baro estis donita de Jeffrey Lagarias en 2002, kiu pruvis ke la rimana hipotezo estas ekvivalento al la frazo ke
por ĉiu natura nombro n, kie estas la n-a harmona nombro.



















