Saltu al enhavo

Historio de fiziko

Pending
El Vikipedio, la libera enciklopedio
Neŭtona pendolo, nomita laŭ fizikisto Isaac Newton.

Fiziko estas branĉo de scienco, kies ĉefaj studobjektoj estas materio kaj energio. Malkovroj de fiziko trovas aplikojn ĉie en natursciencoj kaj en teknologio. Historie, fiziko eliris el la scienca revolucio de la 17-a jarcento, rapide kreskis en la 19-a jarcento, poste estis transformita per serio da malkovroj en la 20-a jarcento. Fiziko hodiaŭ povas esti dividita loze en klasika fiziko kaj moderna fiziko.

Antikva historio

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikolo Historio de astronomio.

Elementoj de kio iĝis fiziko estis tiritaj ĉefe de la kampoj de astronomio, optiko, kaj meĥaniko, kiuj estis metodike unuigitaj tra la studo de geometrio. Tiuj matematikaj disciplinoj komenciĝis en la antikva epoko ĉe la babilonanoj kaj kun helenismaj verkistoj kiel Arkimedo kaj Ptolemeo. Antikva filozofio, dume, inkludis tion, kio estis nomita "Fiziko".

Greka koncepto

[redakti | redakti fonton]

La movo direkte al racia kompreno de naturo komenciĝis almenaŭ ekde la Arkaika periodo en Grekio (650-480 a.K.) kun la antaŭsokrataj filozofoj. La filozofo Taleso el Mileto (7-a kaj 6-a jarcentoj a.K.), sinkronigita "la Patro de Scienco" pro rifuzo akcepti diversajn supernaturajn, religiajn aŭ mitologiajn klarigojn por naturaj fenomenoj, proklamis ke ĉiu okazaĵo havas naturan kaŭzon.[1] Taleso ankaŭ faris progresojn en 580 a.K. sugestante ke akvo estas la baza elemento, eksperimentante kun la altiro inter magnetoj kaj frotita sukceno kaj formulante la unuajn registritajn kosmologiojn. Anaksimandro, ellaboranto de praevolua teorio, kontestis la ideojn de Taleso kaj proponis ke prefere ol akvo, substanco nomita apeiron estis la konstrubriketo de ĉiu materio. Ĉirkaŭ 500 a.K., Heraklito proponis ke la nura baza leĝo reganta la Universon estis la principo de ŝanĝo kaj ke nenio restas en la sama ŝtato senfine. Kune kun lia nuntempa Parmenido estis inter la unuaj akademiuloj en antikva fiziko se temas pri pripensi la rolon de tempo en la universo, ŝlosila koncepto kiu daŭre estas temo en moderna fiziko.

Barato kaj Ĉinio

[redakti | redakti fonton]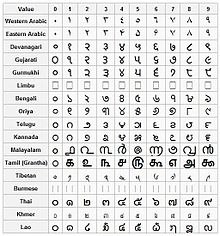
La hindu-araba cifersistemo. La surskriboj sur la ediktoj de Aŝoko (3-a jarcento a.K.) montras tiun nombrosistemon uzatan de la Imperia Maŭrjoj.

Gravaj fizikaj kaj matematikaj tradicioj ankaŭ ekzistis en antikvaj ĉinaj kaj hindaj sciencoj.

Stelmapooj de la 11-ajarcenta ĉina polimatiko Su Song estas la plej malnova konata lignobriketo-presitaj stelmapoj por esti pluvivinta ĝis la nuntempo. Ĉi tiu ekzemplo, datita 1092,[note 1] uzas la cilindran ekvirektangulan projekcion.[2]

En hinda filozofio, Maharishi Kanado estis la unua se temas pri sisteme evoluigi teorion de atomismo ĉirkaŭ 200 a.K.[3] kvankam kelkaj verkintoj asignis al li pli fruan epokon en la 6-a jarcento a.K.[4][5] Ĝi estis plue ellaborita fare de la budhanaj atomistoj Dharmakirti kaj Dignāga dum la 1-a jarmilo p.K.[6] Pakudha Kaccayana, hinda filozofo de la 6-a jarcento a.K. kaj samtempulo de Budho Gotamo, ankaŭ prezentis ideojn pri la atomkonstitucio de la materia mondo. Tiuj filozofoj kredis ke aliaj elementoj (krom etero) estis fizike palpeblaj kaj tial konsistis el minusklaj partikloj de materio. La lasta minuskla partiklo de materio kiu ne povus esti subdividita plu estis nomita Parmanu. Tiuj filozofoj konsideris la atomon nedetruebla kaj tial eterna. La budhanoj opiniis, ke atomoj estas etaj objektoj nevideblaj per la nuda okulo, kiuj estiĝas kaj malaperas en momento. La Vajŝeŝika lernejo de filozofoj kredis ke atomo estas nura punkto en spaco. Ĝi ankaŭ estis unua por prezenti rilatojn inter moviĝo kaj forto aplikita. Hindaj teorioj pri la atomo estas tre abstraktaj kaj enplektitaj en filozofio ĉar ili baziĝis sur logiko kaj ne sur persona sperto aŭ eksperimentado. En hinda astronomio, Aryabhatiya de Aryabhata (499 p.K.) proponis la terrotacion, dum Nilakantha Somayaji (1444-1544) de la Kerala lernejo de astronomio kaj matematiko proponis semi-heliocentran modelon similan al la Tikonia sistemo.

La studo de magnetismo en Antikva Ĉinio devenas de la 4-a jarcento a.K. (en la Libro de la Diablo Vala Majstro),[7] Ĉefa kontribuanto al tiu kampo estis Ŝen Kuo (1031-1095), erudiciulo kaj ŝtatisto kiu estis la unua se temas pri priskribi la magnet-pinglan kompason uzitan por navigado, ankaŭ kiel establado de la koncepto de vera nordo. En optiko, Ŝen Kuo sendepende evoluigis senluman kameron.[8]

Islama mondo

[redakti | redakti fonton]
Ibn al-Haytham (ĉ. 965–1040).

En la 7-a ĝis 15-a jarcentoj, scienca progreso okazis en la islama mondo. Multaj klasikaj verkoj en la hinda, asira, sasana (persa) kaj la greka, inkluzive de la verkoj de Aristotelo, estis tradukitaj en la araban.[9] Gravaj kontribuoj estis faritaj fare de Ibn al-Haytham (965-1040), araba[10] aŭ persa[11] sciencisto, konsiderita kiel fondinto de moderna optiko. Ptolemeo kaj Aristotelo teoriadis ke lumo aŭ brilis de la okulo por prilumi objektojn aŭ ke "formoj" eliris el objektoj mem, dum al-Haytham (konata sub la latina nomo "Alhazen") sugestis ke lumo vojaĝas al la okulo en radioj de malsamaj punktoj. sur objekto. La verkoj de Ibn al-Haitham kaj al-Biruni (973–1050), persa sciencisto, poste pasis al Okcidenteŭropo kie ili estis studitaj fare de akademiuloj kiel ekzemple Roger Bacon kaj Vitello.[12]

Ibn al-Haytham uzis kontrolitajn eksperimentojn en sia laboro pri optiko, kvankam ĝis kia grado ĝi diferencis de Ptolemeo estas debato.[13][14] Arabaj mekanikistoj kiel Bīrūnī kaj Al-Khazini evoluigis sofistikan "sciencon de pezo", aranĝante mezuradojn de specifaj pezoj kaj volumoj.[15]

Ibn Sīnā (980-1037), konata kiel "Aviceno", estis polimatesto de Bukaro (en aktuala Uzbekio) respondeca por gravaj kontribuoj al fiziko, optiko, filozofio kaj medicino. Li publikigis sian teorion de moviĝo en Book of Healing (1020), kie li argumentis ke impeto estas aldonita al kuglo fare de la ĵetanto. Li rigardis ĝin kiel persistan, postulante eksterajn fortojn kiel aerreziston por disipi ĝin.[16][17][18] Ibn Sina faris distingon inter "forto" kaj "inklino" (nomita "mayl"), kaj argumentis ke objekto akiris mayl kiam la objekto estas en opozicio al sia natura moviĝo. Li finis ke daŭrigo de moviĝo ricevas al la inklino kiu estas transdonita al la objekto, kaj tiu objekto estos en moviĝo ĝis la mayl estas elspezita. Tiu koncepto de moviĝo estas kongrua kun la unua leĝo de Neŭtono de moviĝo, inercio, kiu deklaras ke objekto en moviĝo restos en moviĝo krom se ĝi estas agata de ekstera forto.[16] Tiu ideo kiu malsamopiniis de la aristotela vidpunkto estis poste priskribita kiel "impeto" fare de Johano Buridano, kiu estis verŝajne influita per la Libro de Resanigo de Ibn Sina.[19]

Paĝo el Algebro de al-Khwārizmī.

Hibat Allah Abu'l-Barakat al-Baghdaadi (ĉ. 1080 - c. 1165) adoptis kaj modifis la teorion de Ibn Sina pri kuglomovo. En lia Kitab al-Mu'tabar, Abu'l-Barakat deklaris ke la movilo donas perfortan inklinon (mayl qasri) sur la movita kaj ke tio malpliiĝas kiam la moviĝanta objekto distancigas sin de la movilo.[20] Li ankaŭ proponis klarigon de la akcelo de falantaj korpoj per la amasiĝo de sinsekvaj pliigoj de potenco kun sinsekvaj pliigoj de rapideco.[21] Laŭ Shlomo Pines, la teorio de moviĝo de al-Baghdaadi estis "la plej malnova neo de la fundamenta dinamika leĝo de Aristotelo [nome, ke konstanta forto produktas unuforman moviĝon], [kaj estas tiel] antaŭvido en neklara modo de la fundamenta leĝo de klasika mekaniko [nome, ke forto aplikata kontinue produktas akceladon]."[22] Jean Buridan kaj Alberto de Saksio poste rilatis al Abu'l-Barakat en klarigado ke la akcelo de falanta korpo estas rezulto de ĝia kreskanta impeto.[20]

Ibn Bajjah (ĉ.  1085-1138), konata kiel "Avempace" en Eŭropo, proponis ke por ĉiu forto ĉiam ekzistas reakcia forto. Ibn Bajjah estis kritikisto de Ptolemeo kaj li laboris pri kreado de nova teorio de rapideco por anstataŭigi tiun teoriaditan fare de Aristotelo. Du estontaj filozofoj apogis la teoriojn kreitajn de Avempace, konataj kiel Avempacean-dinamiko. Tiuj filozofoj estis Tomaso de Akvino, katolika pastro, kaj Johano Duns Skoto.[23] Galileo daŭriĝis por adopti la formulon de Avempace "ke la rapideco de antaŭfiksita objekto estas la diferenco de la mova forto de tiu objekto kaj la rezisto de la medio de moviĝo".[23]

Nasir ad-Din at-Tusi (1201-1274), persa astronomo kaj matematikisto kiu mortis en Bagdado, prezentis la Tusi-paron. Koperniko poste multe uzis la laboron de ad-Din al-Tusi kaj liaj studentoj, sed sen agnosko.[24]

Mezepoka Eŭropo

[redakti | redakti fonton]

Konscio pri antikvaj verkoj reeniris la Okcidenton per tradukoj de la araba al la latina. Ilia reenkonduko, kombinita kun Jude-islamaj teologiaj komentaĵoj, havis grandan influon sur mezepokaj filozofoj kiel ekzemple Tomaso de Akvino. Skolastikaj eŭropaj akademiuloj, kiuj klopodis akordigi la filozofion de la antikvaj klasikaj filozofoj kun kristana teologio, proklamis Aristotelon la plej granda pensulo de la antikva mondo. En kazoj kie ili ne rekte kontraŭdiris la Biblion, aristotela fiziko iĝis la fundamento por la fizikaj klarigoj de la eŭropaj eklezioj. Kvantigo iĝis kernelemento de mezepoka fiziko.[25]

Surbaze de aristotela fiziko, skolastika fiziko priskribis aferojn kiel moviĝantajn laŭ sia esenca naturo. Ĉielaj objektoj estis priskribitaj kiel moviĝantaj en cirkloj, ĉar perfekta cirkla moviĝo estis konsiderita denaska posedaĵo de objektoj kiuj ekzistis en la nekoruptita sfero de la ĉielaj sferoj. La teorio de impeto, la prapatro al la konceptoj de inercio kaj movokvanto, estis evoluigita laŭ similaj linioj fare de mezepokaj filozofoj kiel ekzemple Johano Filopono kaj Buridano. Movoj sub la luna sfero estis viditaj kiel neperfektaj, kaj tiel ne povus esti atenditaj elmontri konsekvencan moviĝon. Pli idealigita moviĝo en la "subluna" sfero povus nur esti atingita per artifiko, kaj antaŭ la 17-a jarcento, multaj ne rigardis artefaritajn eksperimentojn kiel validan rimedon por lerni pri la natura mondo. Fizikaj klarigoj en la subluna sfero rondiris ĉirkaŭ tendencoj. Ŝtonoj enhavis la elementon tero, kaj teraj objektoj emis moviĝi en rekta linio al la centro de la tero (kaj la universo laŭ la aristotela geocentra vido) krom se alie malhelpite fari tion.[26]

Scienca Revolucio

[redakti | redakti fonton]

Dum la 16-a kaj 17-a jarcentoj, granda progreso de scienca progreso konata kiel la Scienca Revolucio okazis en Eŭropo. Malkontento pri pli malnovaj filozofiaj aliroj komenciĝis pli frue kaj produktis aliajn ŝanĝojn en la socio, kiel ekzemple la Protestanta Reformacio, sed la revolucio en scienco komenciĝis kiam naturfilozofoj komencis fari daŭrantan atakon kontraŭ la Skolastika filozofia programo kaj supozis ke matematika priskriba kabaloj adoptitaj de tiaj kampoj kiel mekaniko kaj astronomio povis fakte doni universale validajn karakterizaĵojn de moviĝo kaj aliajn konceptojn.

Nikolao Koperniko

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikoloj Nikolao Koperniko, Tycho Brahe kaj Johannes Kepler.
La pola astronomo Nikolaus Kopernikus (1473–1543) estas memorita pro sia evoluo de heliocentra modelo de la Sunsistemo .

Trarompo en astronomio faris pola astronomo Nikolao Koperniko (1473–1543) kiam, en 1543, li donis fortajn argumentojn por la heliocentra modelo de la Sunsistemo, ŝajne kiel rimedo por bildigi tabelojn. planeda movo pli preciza kaj simpligi ilian produktadon. En heliocentraj modeloj de la Sunsistemo, la Tero orbitas la Sunon kune kun aliaj korpoj en Tera galaksio, kontraŭdiro laŭ la grek-egipta astronomo Ptolemeo (dua jarcento p.K.; vidu supre) , kies sistemo metis la Teron en la centron de la Universo kaj estis akceptita dum pli ol 1,400 jaroj. La greka astronomo Aristarko el Samoso (Ŝablono:Cirka) sugestis, ke la Tero rondiras ĉirkaŭ la Suno, sed la rezonado de Koperniko kondukis al daŭra ĝenerala akcepto de tiu "revolucia" ideo. La libro de Koperniko prezentanta la teorion (De revolutionibus orbium coelestium, "Sur la Revolucioj de la Ĉielaj Sferoj") estis publikigita ĵus antaŭ lia morto en 1543 kaj, ĉar ĝi nun estas ĝenerale konsiderita marki la komencon de moderna astronomio, ankaŭ estas konsiderata kiel la komenco de la Scienca Revolucio. La nova perspektivo de Koperniko, kune kun la precizaj observaĵoj faritaj de Tycho Brahe, ebligis al germana astronomo Johannes Kepler (1571–1630) formuli liajn leĝojn pri planeda moviĝo tio restas en uzo hodiaŭ.

Galileo Galilei

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikolo Galileo Galilei.
Galileo Galilei, frua propagandanto de la moderna scienca mondkoncepto kaj metodo
(1564–1642)

La itala matematikisto, astronomo, kaj fizikisto Galileo Galilei (1564–1642) estis subtenanto de Kopernikismo kiu faris multajn astronomiajn eltrovaĵojn, faris empiriajn eksperimentojn kaj plibonigis la teleskopon. Kiel matematikisto, la rolo de Galileo en la universitato kulturo de lia epoko estis subigita al la tri ĉefaj studtemoj: juro, medicino, kaj teologio (kiu estis proksime ligita al filozofio). Galileo tamen sentis, ke la priskriba enhavo de la teknikaj fakoj motivis filozofian intereson, precipe ĉar matematika analizo de astronomiaj observaĵoj – precipe, la analizo de Koperniko de la relativa moviĝo de la Suno, Tero, Luno kaj planedoj  – indikis ke la deklaroj de filozofoj pri la naturo de la universo povus montriĝi kiel eraraj. Galileo ankaŭ faris mekanikajn eksperimentojn, insistante ke moviĝo mem – sendepende de ĉu ĝi estis produktita "nature" aŭ "artefarite" (t.e. intence) – havis universale konsekvencajn trajtojn kiuj povus esti priskribitaj matematike.

La fruaj studoj de Galileo ĉe la Universitato de Pizo estis en medicino, sed li baldaŭ estis altirita al matematiko kaj fiziko. Je 19 jaroj, li malkovris (kaj, poste, kontrolis) la izokrona naturon de la pendolo kiam, uzante sian pulson, li tempigis la osciladojn de svingiĝanta lampo en Piza katedralo kaj trovis, ke ĝi restis la sama por ĉiu svingo sendepende de la amplitudo de la svingo. Li baldaŭ iĝis konata per sia invento de hidrostatika pesilo kaj pro sia traktaĵo pri la gravitocentro de solidaj korpoj. Instruante ĉe la Universitato de Pizo (1589–92), li iniciatis siajn eksperimentojn koncerne la leĝojn de korpoj en moviĝo kiuj alportis rezultojn tiel kontraŭdirajn al la akceptitaj instruoj de Aristotelo ke forta antagonismo estis vekita. Li trovis, ke korpoj ne falas kun rapidoj proporcia al siaj pezoj. La rakonto en kiu Galileo laŭdire faligis pezojn de la Inklina Turo de Pizo estas apokrifa, sed li trovis ke la pado de kuglo. estas parabolo kaj estas kreditita kun konkludoj kiuj antaŭvidis leĝoj de movo de Newton (ekz. la nocio de inercio). Inter tiuj estas tio, kio nun nomiĝas Galila relativeco, la unua precize formulita deklaro pri propraĵoj de spaco kaj tempo ekster tridimensia geometrio.

Kompozita muntado komparanta Jupitero (maldekstra flanko) kaj ĝiaj kvar Galilaj lunoj (de supre al malsupre: Io, Eŭropo, Ganimedo, Kalisto).

Galileo estis nomita la "patro de moderna observa astronomio",[27] la "patro de moderna fiziko", la "patro de scienco",[28] kaj "la patro de moderna scienco".[29] Laŭ Stephen Hawking, "Galileo, eble pli ol iu alia ununura persono, respondecis pri la naskiĝo de moderna scienco."[30] Kiel religia ortodokseco dekretis geocentra aŭ tiĥona kompreno de la Suna sistemo, la subteno de Galileo por heliocentrismo provokis polemikon kaj li estis juĝita de la Inkvizicio. Trovita "vehemente suspektinda de herezo", li estis devigita malkonfesi kaj pasigis la reston de sia vivo sub hejmaresto.

La kontribuoj kiujn Galileo faris al observa astronomio inkludas la teleskopan konfirmon de la fazoj de Venuso; lia malkovro, en 1609, de La kvar plej grandaj lunoj de Jupitero (poste donita la kolektivan nomon de la "Galileaj lunoj"); kaj la observado kaj analizo de sunmakulos. Galileo ankaŭ okupiĝis pri aplikatan sciencon kaj teknologion, inventante, inter aliaj instrumentoj, armean kompason. Lia malkovro de la jovianaj lunoj publikiĝis en 1610 kaj ebligis lin akiri la pozicion de matematikisto kaj filozofo ĉe la Medici kortego. Kiel tia, li estis atendita okupiĝi pri debatoj kun filozofoj en la aristotela tradicio kaj ricevis grandan spektantaron por siaj propraj publikaĵoj kiel ekzemple la Discourses and Mathematical Demonstrations Concerning Two New Sciences (publikigita. eksterlande post lia aresto pro la publikigo de Dialogo Pri la Du Ĉefaj Mondaj Sistemoj) kaj La Testisto.[31][32] La intereso de Galileo pri eksperimentado kaj formulado de matematikaj priskriboj de moviĝo establiĝis eksperimentado kiel integra parto de naturfilozofio. Tiu tradicio, kombinante kun la ne-matematika emfazo de la kolekto de "eksperimentaj historioj" de filozofiaj reformistoj kiel ekzemple William Gilbert kaj Francis Bacon, tiris signifan sekvantaron en la jaroj. kaŭzante kaj post la morto de Galileo, inkluzive de Evangelista Torricelli kaj la partoprenantoj en la Accademia del Cimento en Italio; Marin Mersenne kaj Blaise Pascal en Francio; Christiaan Huygens en Nederlando; kaj Robert Hooke kaj Robert Boyle en Anglio.

René Descartes

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikolo René Descartes.
René Descartes
(1596–1650)

La franca filozofo René Descartes (1596–1650) estis bone ligita al, kaj influa ene de, la eksperimentaj filozofiaj retoj de la tago. Descartes havis pli ambician tagordon, aliflanke, kiu estis adaptita al anstataŭigado de la Skolastika filozofia tradicio entute. Pridubante la realecon interpretitan tra la sencoj, Kartezio serĉis reestabli filozofiajn klarigajn kabalojn reduktante ĉiujn perceptitajn fenomenojn al esti atribueblaj al la moviĝo de nevidebla maro de "korpuskloj". (Precipe, li rezervis homan penson kaj Dion de sia skemo, tenante tiujn por esti apartaj de la fizika universo). Proponante ĉi tiun filozofian kadron, Kartezio supozis ke malsamaj specoj de moviĝo, kiel ekzemple tiu de planedoj kontraŭ tiu de teraj objektoj, ne estis fundamente malsamaj, sed estis simple malsamaj manifestiĝoj de senfina ĉeno de korpuskulaj moviĝoj obeantaj universalajn principojn. Precipe influaj estis liaj klarigoj pri cirklaj astronomiaj movoj laŭ la vortica movo de korpuskloj en spaco (Descartes argumentis, laŭ la kredoj, se ne la metodoj, de la Skolastikoj, ke vakuo ne povus ekzisti), kaj lia klarigo de gravito en terminoj de korpuskloj puŝantaj objektojn malsupren.[33][34][35]

Descartes, kiel Galileo, estis konvinkita pri la graveco de matematika klarigo, kaj li kaj liaj anoj estis esencaj figuroj en la evoluo de matematiko kaj geometrio en la 17-a jarcento. Karteziaj matematikaj priskriboj de moviĝo diris ke ĉiuj matematikaj formuliĝoj devis esti pravigeblaj laŭ rekta fizika ago, pozicio tenita fare de Huygens kaj la germana filozofo Gottfried Leibniz, kiuj, sekvante en la Kartezia tradicio, evoluigis sian propran filozofian alternativon al Skolastiko, kiun li skizis en sia 1714 laboro, la Monadologio. Descartes estis nomita la "Patro de Moderna Filozofio", kaj multe da posta Okcidenta filozofio estas respondo al liaj skribaĵoj, kiuj estas studitaj proksime ĝis hodiaŭ. Aparte liaj Meditadoj pri Unua Filozofio daŭre estas norma teksto ĉe la plej multaj universitataj filozofiaj fakoj. La influo de Kartezio en matematiko estas same ŝajna; la Kartezia koordinatsistemo – permesanta al algebraj ekvacioj esti esprimitaj kiel geometriaj formoj en dudimensia koordinatsistemo – estis nomita laŭ li. Li estas kreditita kiel la patro de analitika geometrio, la ponto inter algebro kaj geometrio, grava al la eltrovo de kalkulo kaj analizo.

Christiaan Huygens

[redakti | redakti fonton]
Pli detalaj informoj troveblas en artikolo Christiaan Huygens.
Christiaan Huygens
(1629–1695)

La nederlanda fizikisto, matematikisto, astronomo kaj inventinto Christiaan Huygens (1629–1695) estis la plej elstara sciencisto en Eŭropo inter Galileo kaj Neŭtono. Huygens venis de familio de nobelaro kiu havis gravan pozicion en la nederlanda socio de la 17-a jarcento; tempo en kiu la Nederlanda Respubliko prosperis ekonomie kaj kulture. Ĉi tiu periodo – proksimume inter 1588 kaj 1702 – de la historio de Nederlando ankaŭ estas referita kiel la Nederlanda Ora Epoko, epoko dum la Scienca Revolucio kiam nederlanda scienco estis inter la plej aklamita en Eŭropo. En ĉi tiu tempo, intelektuloj kaj sciencistoj kiel René Descartes, Baruch Spinoza, Pierre Bayle, Antonie van Leeuwenhoek, John Locke kaj Hugo Grotius loĝis en Nederlando . Estis en tiu ĉi intelekta medio kie Christiaan Huygens kreskis. La patro de Christiaan, Constantijn Huygens, estis, krom grava poeto, la sekretario kaj diplomato por la Princoj de Orange. Li konis multajn sciencistojn de sia tempo pro siaj kontaktoj kaj intelektaj interesoj, inkluzive de René Descartes kaj Marin Mersenne, kaj estis pro tiuj kontaktoj ke Christiaan Huygens ekkonsciis pri ilia laboro. Precipe Descartes, kies mekanisma filozofio havos grandegan influon sur la propra laboro de Huygens. Descartes estis poste imponita de la kapabloj kiujn Christiaan Huygens montris en geometrio, kiel estis Mersenne, kiu baptis lin "la nova Arkimedo" (kiu igis Constantijn nomi sian filon "mia malgranda Arkimedo").

Mirinfano, Huygens komencis sian korespondadon kun Marin Mersenne kiam li estis 17-jara. Huygens interesiĝis pri hazardludoj kiam li renkontis la laboron de Fermat, Blaise Pascal kaj Girard Desargues. Estis Blaise Pascal kiu instigas lin verki Van Rekeningh in Spelen van Gluck, kiun Frans van Schooten tradukis kaj publikigis kiel De Ratiociniis in Ludo Aleae en 1657. La libro estas la plej frue konata. scienca traktado de la temo, kaj tiutempe la plej kohera prezento de matematika aliro al hazardludoj. Du jarojn poste Huygens derivis geometrie la nun normajn formulojn en klasika mekaniko por la centripeta- kaj centrifuga forto en sia verko De vi Centrifuga (1659). Ĉirkaŭ la sama tempo esplorado de Huygens en horologio rezultigis la inventon de la pendola horloĝo; trarompo en tempokonservado kaj la plej preciza kronometristo dum preskaŭ 300 jaroj. La teoria esploro pri la funkciado de la pendolo fine kondukis al la publikigo de unu el liaj plej gravaj atingoj: la Horologium Oscillatorium. Tiu ĉi laboro estis publikigita en 1673 kaj iĝis unu el la tri plej gravaj 17-ajarcentaj verkoj pri mekaniko (la aliaj du estante la Diskursoj kaj Matematikaj Demonstraĵoj Rilate al Du Novaj Sciencoj de Galileo (1638) kaj la Philosophiæ Naturalis Principia Mathematica de Neŭtono. (1687) La Horologium Oscillatorium estas la unua moderna traktaĵo en kiu fizika problemo (la akcelita movo de falanta korpo) estas idealigita per aro de parametroj tiam matematike analizita kaj konsistigas unu el la pioniraj verkoj de aplika matematiko.[36][37] Estas tial, Huygens estis nomita la unua teoria fizikisto kaj unu el la fondintoj de moderna matematika fiziko.[38][39] Horologium Oscillatorium de Huygens havis grandegan influon al la historio de fiziko, precipe al la laboro de Isaac Newton, kiu tre admiris la verkon. Ekzemple, la leĝoj de Huygens priskribitaj en la Horologium Oscillatorium estas strukture la samaj kiel la unuaj du leĝoj de moviĝo.[40]

Kvin jarojn post la publikigo de lia Horologium Oscillatorium, Huygens priskribis sian ondoteorion de lumo. Kvankam proponite en 1678, ĝi ne estis publikigita ĝis 1690 en lia Traité de la Lumière. Lia matematika lumteorio estis komence malaprobita en favoro de la korpuskula teorio de Neŭtono pri lumo, ĝis Augustin-Jean Fresnel adoptis la principon de Huygens por doni kompletan klarigon de la rektliniaj disvastigaj kaj difrakto-efikoj de lumo en 1821. Hodiaŭ ĉi tiu principo. estas konata kiel la Huygens-Fresnel-principo. Kiel astronomo, Huygens komencis mueli lensojn kun sia frato Constantijn jr. konstrui teleskopojn por astronomia esplorado. Li estis la unua se temas pri identigi la ringojn de Saturno kiel "maldika, plata ringo, nenie tuŝanta, kaj inklina al la ekliptiko", kaj malkovris la unuan el la lunoj de Saturno, Titano , uzante refrakta teleskopo.

Krom la multaj gravaj malkovroj kiujn Huygens faris en fiziko kaj astronomio, kaj liaj inventoj de spritaj aparatoj, li ankaŭ estis la unua kiu alportis matematikan rigoron al la priskribo de fizikaj fenomenoj. Pro tio, kaj la fakto ke li evoluigis instituciajn kadrojn por scienca esplorado sur la kontinento, li estis referita kiel "la ĉefa aktoro en 'kreado de scienco en Eŭropo'.

Isaac Newton

[redakti | redakti fonton]
Sir Isaac Newton
(1642–1727)

La malfruaj 17-a kaj fruaj 18-a jarcentoj vidis la atingojn de Universitato de Kembriĝo fizikisto kaj matematikisto Sir Isaac Newton (ofte esperantigita kiel Siro Isaako Neŭtono, 1642-1727). Neŭtono, ulo de la Reĝa Societo de Anglio, kombinis siajn proprajn eltrovaĵojn en mekaniko kaj astronomio al pli fruaj por krei ununuran sistemon por priskribi la funkciadon de la universo. Neŭtono formulis tri leĝojn de moviĝo, kiuj formulis la rilaton inter moviĝo kaj objektoj kaj ankaŭ la leĝon de universala gravitado, ĉi-lasta el kiuj povus esti uzata por klarigi la konduton ne nur de falantaj korpoj sur la tero sed ankaŭ planedoj kaj aliaj ĉielaj korpoj. Por alveni al siaj rezultoj, Neŭtono inventis unu formon de tute nova branĉo de matematiko: kalkulo (ankaŭ inventita sendepende fare de Gottfried Leibniz), kiu devis iĝi esenca ilo en granda parto de la pli posta evoluo en la plej multaj branĉoj de fiziko. La trovoj de Neŭtono estis prezentitaj en lia Philosophiæ Naturalis Principia Mathematica ("Matematikaj Principoj de Natura Filozofio"), kies publikigo en 1687 markis la komencon de la moderna periodo de mekaniko kaj astronomio.

Neŭtono povis refuti la kartezian mekanikan tradicion ke ĉiuj moviĝoj devus esti klarigitaj kun respekto al la tuja forto penita per korpuskloj. Uzante siajn tri leĝojn de moviĝo kaj leĝon de universala gravitado, Neŭtono forigis la ideon ke objektoj sekvis padojn determinitajn per naturaj formoj kaj anstataŭe pruvis ke ne nur regule observitaj padoj, sed ĉiuj estontaj movoj de iu korpo povus esti deduktitaj matematike surbaze de scio pri ilia ekzistanta movo, ilia maso, kaj la fortoj agantaj sur ili. Tamen, observitaj ĉielaj movoj ne precize konformiĝis al neŭtona traktado, kaj Neŭtono, kiu ankaŭ estis profunde interesita pri teologio, imagis, ke Dio intervenas por certigi la daŭran stabilecon de la sunsistemo.

Gottfried Leibniz
(1646–1716)

La principoj de Neŭtono (sed ne liaj matematikaj traktadoj) pruvis kontestataj kun Kontinentaj filozofoj, kiuj trovis lian mankon de metafizika klarigo por movado kaj gravitado filozofie neakceptebla. Komenciĝante ĉirkaŭ 1700, amara fendiĝo malfermiĝis inter la kontinentaj kaj britaj filozofiaj tradicioj, kiuj estis ekscititaj per ekscititaj, daŭrantaj, kaj brutale personaj disputoj inter la anoj de Neŭtono kaj Leibniz koncerne prioritaton super la analizaj teknikoj de kalkulado, kiujn ĉiu evoluigis sendepende. Komence, la karteziaj kaj leibniziaj tradicioj regis sur la Kontinento (kaŭzante la dominecon de la leibniziana kalkulnotacio ĉie krom Britio). Neŭtono mem restis private ĝenita ĉe la manko de filozofia kompreno de gravitado insistante en siaj skribaĵoj ke neniu estis necesa por konkludi ĝian realecon. Dum la 18-a jarcento progresis, Kontinentaj naturfilozofoj ĉiam pli akceptis la volon de la neŭtonanoj rezigni ontologiajn metafizikajn klarigojn por matematike priskribitaj movoj.[41][42][43]

Neŭtono konstruis la unuan funkciantan spegulteleskopon[44] kaj evoluigis teorion de koloro, publikigita en Opticks, surbaze de la observado ke prismo malkomponas blankan lumon en la multajn kolorojn formantajn la videblan spektron. Dum Neŭtono klarigis lumon kiel estante kunmetita de etaj partikloj, rivala teorio de lumo kiu klarigis ĝian konduton laŭ ondoj estis prezentita en 1690 fare de Christiaan Huygens. Tamen, la kredo je la mekanisma filozofio kunligita kun la reputacio de Neŭtono signifis ke la ondoteorio vidis relative malmulte da subteno ĝis la 19-a jarcento. Neŭtono ankaŭ formulis empirian leĝon de malvarmigo, studis la rapidon de sono, esploris potencoserion, montris la ĝeneraligitan binoman teoremon kaj evoluigis metodon por aproksimado de la radikoj de funkcio. Lia laboro pri senfinaj serioj estis inspirita per la decimaloj de Simon Stevin.[45] Plej grave, Neŭtono montris, ke la movoj de objektoj sur la Tero kaj de ĉielaj korpoj estas regataj de la sama aro de naturaj leĝoj, kiuj estis nek kapricaj nek malbonvolaj. Demonstrante la konsistencon inter la leĝoj de Kepler pri planeda moviĝo kaj sia propra gravita teorio, Neŭtono ankaŭ forigis la lastajn dubojn pri heliocentrismo. Kunvenante ĉiujn ideojn prezentitajn dum la Scienca Revolucio, Neŭtono efike establis la fundamenton por moderna socio en matematiko kaj scienco.

Moderna historio

[redakti | redakti fonton]

La fiziko en sia moderna signifo naskiĝis en la 16-a jarcento, per la uzo de eksperimentado kaj observado fare de homoj kiel Galileo Galilei, kiu estas ĝenerale konsiderata kiel la patro de la fizika scienca metodo.

En la 17-a jarcento okazis forta antaŭeniro de la Fiziko danke al la rezultoj atingitaj de Newton kiu formulis la ĉefajn leĝojn de la dinamiko (leĝoj de Newton) kaj la gravito, krom la disvolvo de diversaj laboroj en la kampo de la optiko.

La 18-a jarcento vidis la disvolvon de aliaj disciplinoj kiel termodinamiko, statistika mekaniko kaj fiziko de fluaĵoj.

En la 19-a jarcento disvolviĝas avancoj revoluciaj en la fakoj pri elektro kaj magnetismo. En 1855 Maxwell unuigis ambaŭ fenomenojn kaj kreis novan Teorion de Elektromagnetismo. Ĝi ankaŭ provokis fortan ŝanĝon en la kompreno de la teorio de la lumo.

Fine de tiu jarcento kaj komence de la 20-a malkovriĝas diversajn radiadojn, ĝis nun nekonatajn, kaj oni faras gravajn malkovrojn rilate al la elementaj partikloj. Tio kondukas al la naskiĝo de revolucia kampo: la nuklea fiziko.

Notoj

[redakti | redakti fonton]
  1. ↑ Alklaku la bildon por vidi pliajn detalojn.

Referencoj

[redakti | redakti fonton]
  1. ↑ "This shift from ecclesiastical reasoning to scientific reasoning marked the beginning of scientific methodology." Singer, C., A Short History of Science to the 19th Century, Streeter Press, 2008, p. 35.
  2. ↑ Miyajima, Kazuhiko (1998), "Projection Methods in Chinese, Korean and Japanese Star Maps", Highlights of Astronomy 11 (2): 712–715, doi:10.1017/s1539299600018554 
  3. ↑ Oliver Leaman, Key Concepts in Eastern Philosophy. Routledge, 1999, page 269.
  4. ↑ Chattopadhyaya 1986, paĝoj 169–70
  5. ↑ Choudhury 2006, p. 202
  6. ↑ (Stcherbatsky 1962 (1930). Vol. 1. P. 19)
  7. ↑ Li Shu-hua, "Origine de la Boussole 11. Aimant et Boussole", Isis, Vol. 45, No. 2. (Jul., 1954), p.175
  8. ↑ Joseph Needham, Volume 4, Part 1, 98.
  9. ↑ (1996) Robinson, Francis: The Cambridge Illustrated History of the Islamic World. Cambridge University Press, p. 228–229.
  10. ↑ Esposito (2000)، The Oxford History of Islam، Oxford University Press، P. 192. : “Ibn al-Haytham (d. 1039), known in the West as Alhazan, was a leading Arab mathematician, astronomer, and physicist. His optical compendium, Kitab al-Manazir, is the greatest medieval work on optics”
  11. ↑ Ŝablono:Harvard citation, Ŝablono:Harvard citation, Understanding History by John Child, Paul Shuter, David Taylor - Page 70. "Alhazen, a Persian scientist, showed that the eye saw light from other objects. This started optics, the science of light. The Arabs also studied astronomy, the study of the stars. "
  12. ↑ Glick, Livesey & Wallis (2005, pp. 89–90)
  13. ↑ Smith, Mark. (2015) From Sight to Light: The Passage from Ancient to Modern Optics. The University of Chicago Press, p. 225. “The same holds for Alhacen’s methodology. It may look modern because of its strong empirical bias and reliance on controlled experiments, but Ptolemy’s approach was no less empirical, and it, too, was based on controlled experiments. In addition, Alhacen’s two most modern-looking experiments are based on physically unobtainable precision in equipment design and observation, so we are left to doubt that he actually carried them out as described— except, of course, in his mind. And these experiments were not new in conception. They were clearly based on equivalent ones in Ptolemy’s Optics, although Alhacen had to reformulate them in significant and creative ways to accommodate the testing of light rays rather than visual rays.”.
  14. ↑ Darrigol, Olivier. (2012) A History of Optics from Greek Antiquity to the Nineteenth Century. Oxford University Press, p. 20.
  15. ↑ Lindberg, David. (2013) The Cambridge History of Science, Volume 2, Medieval Science, p. 984–1108.
  16. ↑ 16,0 16,1 (2005) “An analysis of the historical development of ideas about motion and its implications for teaching”, Physics Education 40 (2), p. 141. doi:10.1088/0031-9120/40/2/002. Bibkodo:2005PhyEd..40..139E. 250809354. 
  17. ↑ Seyyed Hossein Nasr & Mehdi Amin Razavi. (1996) The Islamic intellectual tradition in Persia. Routledge. ISBN 978-0-7007-0314-2.
  18. ↑ Aydin Sayili (1987). “Ibn Sīnā and Buridan on the Motion of the Projectile”, Annals of the New York Academy of Sciences 500 (1), p. 477–482. doi:10.1111/j.1749-6632.1987.tb37219.x. Bibkodo:1987NYASA.500..477S. 84784804. 
  19. ↑ Sayili, Aydin. "Ibn Sina and Buridan on the Motion the Projectile". Annals of the New York Academy of Sciences vol. 500(1). p.477-482.
  20. ↑ 20,0 20,1 Gutman, Oliver. (2003) Pseudo-Avicenna, Liber Celi Et Mundi: A Critical Edition. Brill Publishers. ISBN 90-04-13228-7.
  21. ↑ Crombie, Alistair Cameron, Augustine to Galileo 2, p. 67.
  22. ↑ “Abu'l-Barakāt al-Baghdādī, Hibat Allah”, Dictionary of Scientific Biography.
    (cf. Abel B. Franco (October 2003). "Avempace, Projectile Motion, and Impetus Theory", Journal of the History of Ideas 64 (4), p. 521-546 [528].)
  23. ↑ 23,0 23,1 Gracia, Jorge J. E. (2007-11-26), "Philosophy in the Middle Ages: An Introduction", A Companion to Philosophy in the Middle Ages, Blackwell Publishing Ltd, pp. 1–11, doi:10.1002/9780470996669.ch1, (ISBN 9780470996669) 
  24. ↑ Top 10 ancient Arabic scientists. Cosmos magazine (2011-01-06). Alirita 2013-04-20 .
  25. ↑ (1961) “Quantification in Medieval Physics”, Isis 52 (2), p. 143–160. doi:10.1086/349467. 
  26. ↑ Lindberg, David C.. (1992) The Beginnings of Western Science. University of Chicago Press. doi:10.7208/chicago/9780226482064.001.0001. ISBN 978-0-226-48231-6.
  27. ↑
    Citaĵo
    „  ”
    , paĝo 217.
  28. ↑
    Citaĵo
    „  ”
  29. ↑ Finocchiaro (2007).
  30. ↑ (2009) “Galileo kaj la Naskiĝo de Moderna Scienco” 24, p. 36. Alirita 2020-09-15.. 
  31. ↑ Drake (1978)
  32. ↑ Biagioli (1993)
  33. ↑ Shea (1991)
  34. ↑ Garber (1992)
  35. ↑ Gaukroger (2002)
  36. ↑ Ŝablono:Citu libro
  37. ↑ Bruce, I. (2007). Christian Huygens: Horologium Oscillatorium. Tradukita kaj komentita de Ian Bruce.
  38. ↑ Dijksterhuis, F.J. (2008) Stevin, Huygens kaj la nederlanda respubliko. Nieuw archief voor wiskunde, 5, pp 100–107.[1]
  39. ↑ Andriesse, C.D. (2005) Huygens: La Viro Malantaŭ la Principo. Cambridge University Press. Kembriĝo: 6
  40. ↑ Ŝablono:Cita libro
  41. ↑ Hall (1980)
  42. ↑ Bertolini Meli (1993)
  43. ↑ Guicciardini (1999)
  44. ↑ Raymond N. Wilson. (2013) “1.1 Period 1608-1672”, Reflecting Telescope Optics I: Basic Design Theory and its Historical Development. Springer, p. 1–10. ISBN 978-3-662-03227-5.
  45. ↑ Błaszczyk, Piotr; Katz, Mikhail; Sherry, David (2012), "Ten misconceptions from the history of analysis and their debunking", Foundations of Science 18: 43–74, doi:10.1007/s10699-012-9285-8 

Vidu ankaŭ

[redakti | redakti fonton]
Bibliotekoj
Elŝutita el "https://eo.wikipedia.org/w/index.php?title=Historio_de_fiziko&oldid=8961498"